Геометрически поле направлений можно изобразить,
проводя в каждой точке области Д отрезок единичной длины с центром в этой
точке, образующий с положительным направлением оси ![]() угол
угол ![]() (где
(где ![]() ). Если
в точке
). Если
в точке ![]() правая часть уравнения (1.31) обращается в
бесконечность, то направление поля параллельно оси ординат (так как
правая часть уравнения (1.31) обращается в
бесконечность, то направление поля параллельно оси ординат (так как ![]() при
при 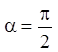 ). Если
в точке
). Если
в точке ![]()
![]() обращается в
неопределённость
обращается в
неопределённость ![]() , то поле направлений в этой точке
не определено, а сама точка называется особой точкой дифференциального
уравнения.
, то поле направлений в этой точке
не определено, а сама точка называется особой точкой дифференциального
уравнения.
Теперь в геометрической интерпретации задачу интегрирования дифференциального уравнения (1.31) можно сформулировать так: найти такие кривые, касательные к которым в каждой точке совпадают с направлением поля в этой точке.
Геометрическое истолкование уравнения (1.31) служит основой для построения приближенных методов решения уравнения (1.31). Один из таких методов называется методом изоклин. Изоклиной поля направлений называется геометрическое место точек, в которых направление поля одинаково. Уравнением изоклины будет линия
![]() ,
, ![]() (1.32)
(1.32)
или ![]() . Метод
изоклин приближенного решения дифференциального уравнения 1-го порядка можно
представить так.
. Метод
изоклин приближенного решения дифференциального уравнения 1-го порядка можно
представить так.
Пусть дано дифференциальное уравнение (1.31) с
начальным условием ![]() . Допустим, уравнение имеет
единственное решение
. Допустим, уравнение имеет
единственное решение ![]() . Разобьем кривую на
. Разобьем кривую на ![]() частей и каждую часть кривой заменим
отрезком касательной в определённых точках кривой. Интегральную кривую теперь
можно заменить ломаной, состоящей из отрезков касательных. Отрезки касательных
получают в методе изоклин из уравнения (1.32).
частей и каждую часть кривой заменим
отрезком касательной в определённых точках кривой. Интегральную кривую теперь
можно заменить ломаной, состоящей из отрезков касательных. Отрезки касательных
получают в методе изоклин из уравнения (1.32).
П р и м е р 1. Дано уравнение 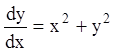 и
начальное условие
и
начальное условие ![]() . Построить изоклины и
приближенное частное решение.
. Построить изоклины и
приближенное частное решение.
Р е ш е н и е. Построим изоклины, полагая ![]() равной
равной ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
Получим уравнение изоклин – линий с одинаковым наклоном касательных:
.
Получим уравнение изоклин – линий с одинаковым наклоном касательных:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
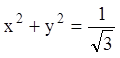 ;
; 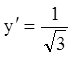 ;
; 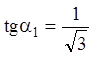 ;
; ![]() ;
;
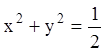 ;
; 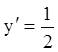 ;
; 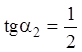 ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Нам известна одна точка интегральной кривой ![]() . В этой точке угол, составленный
касательной с осью
. В этой точке угол, составленный
касательной с осью ![]() ,
, ![]() .
Проведём из точки
.
Проведём из точки ![]() отрезок касательной
отрезок касательной ![]() (до пересечения с ближайшей изоклиной). Из
полученной точки пересечения
(до пересечения с ближайшей изоклиной). Из
полученной точки пересечения ![]() построим отрезок
касательной под углом
построим отрезок
касательной под углом ![]() до пересечения со следующей
изоклиной в точке
до пересечения со следующей
изоклиной в точке ![]() . Из точки
. Из точки ![]() строим отрезок касательной под углом
строим отрезок касательной под углом ![]() до пересечения со следующей изоклиной в
точке
до пересечения со следующей изоклиной в
точке ![]() и так далее. В результате получаем ломаную
и так далее. В результате получаем ломаную
![]() , которая приближённо представляет решение
данного уравнения. Эта ломаная тем точнее будет представлять решение уравнения,
чем гуще будут изоклины.
, которая приближённо представляет решение
данного уравнения. Эта ломаная тем точнее будет представлять решение уравнения,
чем гуще будут изоклины.
З а м е ч а н и е 1. Используя метод изоклин, можно
строить приближенно и общие решения уравнения (1.31). Этот метод позволяет
определить характерные линии и области поля интегральных кривых, такие,
например, как область возрастания (при ![]() ),
убывания (при
),
убывания (при ![]() ) интегральных кривых, линии
экстремумов (
) интегральных кривых, линии
экстремумов (![]() ). Если к тому же функция
). Если к тому же функция ![]() в уравнении (1.31) дифференцируема, то при
помощи неявного задания второй производной
в уравнении (1.31) дифференцируема, то при
помощи неявного задания второй производной
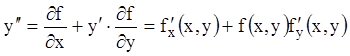 (1.33)
(1.33)
можно,
положив, ![]() определить область выпуклости – вогнутости
(
определить область выпуклости – вогнутости
(![]() ,
, ![]() ) и точки
перегиба интегральных кривых (
) и точки
перегиба интегральных кривых (![]() ).
).
П р и м е р 2. Построить приближённо интегральные
кривые уравнения ![]() , используя метод изоклин.
, используя метод изоклин.
Р е ш е н и е. Записываем уравнение изоклин (![]() ):
): ![]() ,
откуда
,
откуда 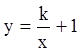 - семейство гипербол.
- семейство гипербол.
1) При ![]() имеем
имеем ![]()
![]() или
или ![]() .
.
Таким образом, прямая ![]() - линия
экстремумов (линия
- линия
экстремумов (линия ![]() не линия экстремумов, так как
является частным решением уравнения, и на основании теоремы существования и
единственности решения через её точки не могут проходить другие интегральные
кривые).
не линия экстремумов, так как
является частным решением уравнения, и на основании теоремы существования и
единственности решения через её точки не могут проходить другие интегральные
кривые).
2) Интервалы возрастания – убывания:
Возрастания: 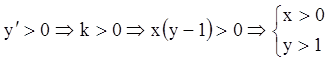 или
или 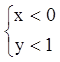 .
.
Убывания: 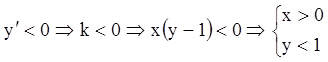 или
или 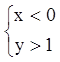 .
.
3) Интервалы выпуклости – вогнутости (смотрите формулу (2.6)).
![]() .
.
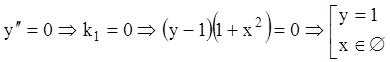 - частное решение
- частное решение
![]() - выпуклость вниз
- выпуклость вниз
![]() - выпуклость вверх
- выпуклость вверх
ЛЕКЦИЯ №2.
тема: 2. Дифференциальные уравнения с разделенными и разделяющимися переменными. Однородные дифференциальные уравнения и к ним сводящиеся.
2.1 Основные понятия. Задача Коши
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.