Дифференциальные уравнения и математическое моделирование. Основные понятия дифференциальных уравнений. Метод Изоклин, страница 23

где  - непрерывная функция, имеющая непрерывные частные производные первого порядка и такая, что

.

Следовательно, функция  - непрерывна в области  и удовлетворяет по переменной y условиям теоремы существования и единственности решения для уравнений, разрешенных относительно y'. Значит, существует в интервале  единственное решение уравнения (5.96) , а значит, и уравнение (5.7) такое, что .

Покажем теперь, что . Действительно, так как есть решение уравнения (5.96) и , то при  имеем тождество

.

Полагая здесь , получим

,

т.е. , что и требовалось доказать.

Точка , в окрестности которой задача Коши для уравнения (5.7) имеет единственное решение, называется обыкновенной точкой данного уравнения.

Точка , в которой нарушается единственность решения задачи Коши для уравнения (5.7), называется особой точкой данного уравнения.

ЛЕКЦИЯ №6.

Тема: 6. ОСОБЫЕ ТОЧКИ И ОСОБЫЕ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА

ПЛАН

6.1 Особые точки дифференциальных уравнений первого порядка

6.2 Особые решения дифференциальных уравнений первого порядка вида

6.3 Особые решения для уравнений

6.1 Особые точки дифференциальных уравнений первого порядка

Как было сказано выше, точка , в окрестности которой задача Коши для дифференциального уравнения первого порядка имеет единственное решение, называется обыкновенной точкой данного уравнения. Точка , в которой нарушается единственность решения задачи Коши для уравнения первого порядка, называется особой точкой данного уравнения.

Таким образом, особые точки дифференциального уравнения первого порядка следует искать среди тех точек, в которых нарушается хотя бы одно из условий теоремы существования. Конечно, не каждая точка, в которой нарушается условие теоремы  существования и единственности решения, обязательно является особой, т.к. условия этой теоремы достаточны для существования и единственности, но они не являются необходимыми.

Предположим, что для уравнения вида

                                                            (6.1)

нарушено первое условие теоремы существования: функция  в точке  не является непрерывной. Тогда возможны следующие случаи:

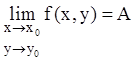, где А – конечное число, но ;

;

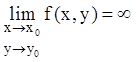 не имеет ни конечного, ни бесконечного предела в точке .

Первые два случая можно свести к случаю, рассмотренному теоремой существования. В частности, в 1) функцию  доопределяют так, чтобы она стала непрерывной в этой точке (). В случае 2) вместо уравнения (6.1) рассматривают уравнение:

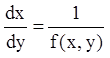.                                                       (6.2)

Положив 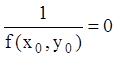, приходим к тому, что уравнение (6.2) имеет единственное решение с вертикальной касательной в точке .

Рассмотрим случай 3). В этом случае точку , в которой 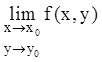  не существует, называют изолированной особой точкой уравнения (6.1).

Особенно часто приходится рассматривать уравнения вида

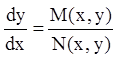                                                        (6.3)

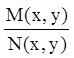где функции  и  непрерывны. В этом случае функции  и 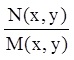  будут одновременно разрывными лишь в тех точках , в которых  и не существует пределов

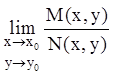 и  .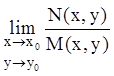

Такие точки называют изолированными особыми точками типа . (Особая точка называется изолированной, если в некоторой ее окрестности нет других особых точек этого уравнения).

Рассмотрим поведение интегральных кривых в окрестности изолированной особой точки однородного уравнения:

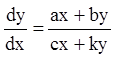,                                                                 (6.4)

где , причем такие, что (если  , то уравнение (6.4) вырождается в уравнение 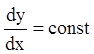). Очевидно, что точка (0,0) является изолированной особой точкой уравнения (6.4). Так как правая часть уравнения (6.4) или правая часть уравнения:

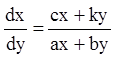                                                        (6.5)

в любой замкнутой окрестности точки  , где , является функцией непрерывной и удовлетворяет в этой точке соответственно по переменной y, или по переменной x условию Липшица, то через каждую такую точку будет проходить только одна интегральная кривая уравнений (6.4) или (6.5). Исследуем поведение интегральных кривых уравнения (6.4) вблизи особой точки О(0,0).