Дифференциальные уравнения и математическое моделирование. Основные понятия дифференциальных уравнений. Метод Изоклин, страница 29

П р и м е р 9. Найти особое решение дифференциального уравнения 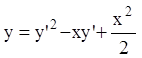, зная его общий интеграл .

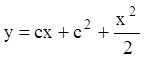Р е ш е н и е. Составляем систему (6.45):

,    .

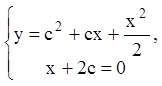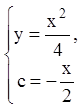Тогда 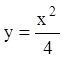  - с-дискриминантная кривая. Исключаем точки, в которых 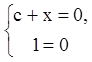 таких нет. Значит, 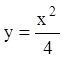 - особое решение.

З а м е ч а н и е. Объединяя первый и второй способы нахождения особых решений можно предложить третий алгоритм их нахождения:

используя систему (6.38), строим р-дискриминантную кривую уравнения;

зная общее решение уравнения, строим с-дискриминантную кривую;

совпадающие РДК и СДК будут особыми решениями.

П р и м е р 10. Найти особые решения уравнения:

,

если его общий интеграл .

Р е ш е н и е. Находим РДК:

 

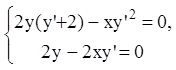
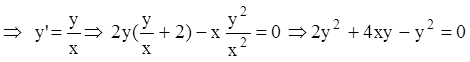
- р-дискриминантная кривая. и .

Подстановкой убеждаемся, что обе функции являются решениями исходного уравнения.

Чтобы установить, являются ли полученные решения особыми, строим СДК.

.

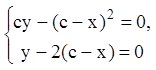Исключаем параметр с:  .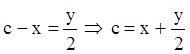  

Тогда:

, 

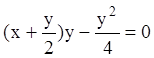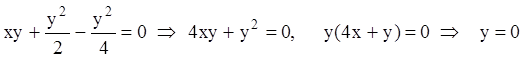
и , что совпадает с ранее полученным. Т.к. на этих линиях выполняются условия  и , а значит,  и  - особые решения заданного уравнения.

ЛЕКЦИЯ №7.

тема: 7. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ

ПЛАН

7.1     Основные понятия и теорема существования

7.2     Некоторые типы уравнений n-го порядка, интегрируемые в квадратурах

7.3     Понижение порядка дифференциального уравнения

7.1 Основные понятия и теорема существования

Обыкновенным дифференциальным уравнением n–го порядка называется уравнение, связывающее неизвестную функцию y, независимую переменную x и производные функции y по x до n-го порядка включительно:

,                                                              (7.1)

здесь F – непрерывная функция всех своих аргументов.

Если выполняются условия теоремы существования неявной функции, а именно – в окрестности значений  , имеют место:

1)  - непрерывная функция своих аргументов;

2)  ;

3) 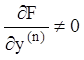 при  , то в окрестности этих значений  уравнение (7.1) можно разрешить относительно , т.е.:

,                                    (7.2)

где f – непрерывная функция всех своих аргументов.

Понятия решения, общего и частного решения, общего и частного интеграла уравнения (7.1) были даны в начале курса. Например, решением уравнения (7.1) на интервале называется функция , определенная и n раз непрерывно дифференцируемая на , если она обращает уравнение (7.1), в тождество:

,

справедливое при всех значениях . Всякому решению уравнения (7.1) на плоскости соответствует некоторая линия – интегральная кривая. Если уравнение первого порядка задает некоторое общее свойство семейства касательных всех его интегральных кривых, то каждое уравнение n-го порядка тоже выражает собой некоторое общее геометрическое свойство всех его интегральных кривых. В частности, всякое уравнение второго порядка:

                                          (7.3)

можем представить в виде 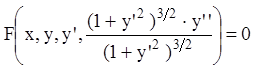, или 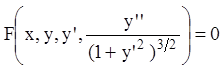, откуда следует связь между координатами, наклоном касательной и кривизной в каждой точке интегральной кривой (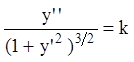 - кривизна кривой ).

Рассматривая прямолинейное движение материальной точки М по оси OX, трактуя x, x', x" как соответственно положение, скорость, ускорение точки М в момент времени t, а функцию как силу, действующую на точку, зависящую от времени, положения и скорости точки (масса точки равна единице), мы, согласно второму закону Ньютона, будем иметь дифференциальное уравнение второго порядка:

,                                  (7.4)

определяющее закон движения точки по оси OX. Всякое решение уравнения (7.4)  соответствует некоторому движению точки М по прямой OX и называется движением.

Задачей Коши для дифференциального уравнения (7.2) называют задачу нахождения такого решения  уравнения (7.2), для которого функция  и ее производные до (n-1)-го порядка включительно принимают в точке  заданные значения

,    (7.5)

называемые начальными условиями этого решения.

Характерной особенностью задачи Коши является то, что условия, которые накладываются на искомое решение, задаются при одном и том же значении независимой переменной .