Вообще говоря, каждой кривой семейства (1.17)
соответствует определённое значение параметра ![]() . Именно
этим отличаются кривые семейства одна от другой. Поставим задачу: составить
дифференциальное уравнение этого семейства кривых, которое описывало бы
свойства, присущие всем кривым данного семейства.
. Именно
этим отличаются кривые семейства одна от другой. Поставим задачу: составить
дифференциальное уравнение этого семейства кривых, которое описывало бы
свойства, присущие всем кривым данного семейства.
Предположим, что функция ![]() -
дифференцируема. Пусть соотношение (1.17) задаёт нашу дифференцируемую функцию
от
-
дифференцируема. Пусть соотношение (1.17) задаёт нашу дифференцируемую функцию
от ![]() :
: ![]() , т. е.
для функции
, т. е.
для функции ![]() из (1.17) выполнены условия теоремы
существования неявной функции. Тогда дифференцируя (1.17), получаем
из (1.17) выполнены условия теоремы
существования неявной функции. Тогда дифференцируя (1.17), получаем
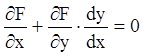 . (1.18)
. (1.18)
Если (1.18) не содержит ![]() , то оно
и будет искомым дифференциальным уравнением семейства кривых.
, то оно
и будет искомым дифференциальным уравнением семейства кривых.
Но исключение ![]() из
(1.17) путём дифференцирования возможно только в частных случаях. А в общем
случае соотношение (1.18) содержит
из
(1.17) путём дифференцирования возможно только в частных случаях. А в общем
случае соотношение (1.18) содержит ![]() . Тогда исключить
параметр
. Тогда исключить
параметр ![]() можно, составив систему из соотношений
(1.17) и (1.18):
можно, составив систему из соотношений
(1.17) и (1.18):
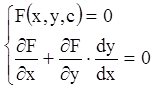 .
.
В результате получим дифференциальное уравнение
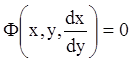 , (1.19)
, (1.19)
которое описывает свойства, присущие всем кривым семейства (1.17).
Т. о., дифференциальное уравнение можно получить формальным исключением параметра из уравнения однопараметрического семейства кривых.
Напоминаем теорему существования неявной функции: если
функция ![]() непрерывна вместе с частными производными
первого порядка в некоторой окрестности точки
непрерывна вместе с частными производными
первого порядка в некоторой окрестности точки ![]() и
и ![]() ,
, ![]() , то
существует такая окрестность точки
, то
существует такая окрестность точки ![]() , в которой уравнение
, в которой уравнение ![]() определяет
определяет ![]() как
однозначную функцию от
как
однозначную функцию от ![]() :
: ![]() ,
обладающую следующими свойствами:
,
обладающую следующими свойствами:
1) ![]() непрерывна вместе с
непрерывна вместе с ![]() ;
;
2) ![]() .
.
П р и м е р 1. Составить дифференциальное уравнение семейства парабол
![]() . (1.20)
. (1.20)
Р е ш е н и е. Дифференцируем (1.20): ![]() ,
, ![]() . Из
системы
. Из
системы 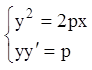 исключаем
исключаем ![]() :
:
![]() или
или ![]() . (1.21)
. (1.21)
Это и есть искомое дифференциальное уравнение.
Заметим, что полученному уравнению (1.21) удовлетворяют и полупрямые ![]() (
(![]() ), не
входящие в данное семейство парабол.
), не
входящие в данное семейство парабол.
Аналогично дифференциальное уравнение 2-го порядка
можно получить, исключая параметры ![]() ,
, ![]() из двухпараметрической семьи плоских
кривых:
из двухпараметрической семьи плоских
кривых:
![]() .
(1.22)
.
(1.22)
Дифференцируя по ![]() ,
получаем:
,
получаем:
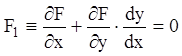 . (1.23)
. (1.23)
В общем случае из (1.22), (1.23) нельзя исключить обе
постоянные, поэтому продифференцировав по ![]() ещё
раз, получим:
ещё
раз, получим:
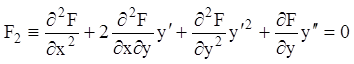 . (1.24)
. (1.24)
Исключая из равенств (1.22)-(1.24) ![]() и
и ![]()
![]() ,
, ![]() (1.25)
(1.25)
и подставляя (1.25) в (1.22), получаем дифференциальное уравнение 2-го порядка:
![]() . (1.26)
. (1.26)
П р и м е р 2. Составить дифференциальное уравнение семейства кривых:
![]() .
(1.27)
.
(1.27)
Р е ш е н и е. Так как уравнение семейства содержит 2
параметра, то дифференцируем его 2 раза, считая что ![]() :
:
![]() , (1.28)
, (1.28)
![]() . (1.29)
. (1.29)
Исключаем ![]() и
и ![]() из системы (1.27)-(1.29). Из уравнения
(1.28) находим
из системы (1.27)-(1.29). Из уравнения
(1.28) находим ![]() и подставляем его в (1.27).
Получаем
и подставляем его в (1.27).
Получаем
![]() .
(1.30)
.
(1.30)
Исключаем ![]() . Из уравнения (1.29)
имеем
. Из уравнения (1.29)
имеем 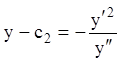 . Подставляя это в (1.30), получаем искомое
дифференциальное уравнение
. Подставляя это в (1.30), получаем искомое
дифференциальное уравнение 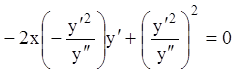 . Преобразуем последнее
уравнение:
. Преобразуем последнее
уравнение: 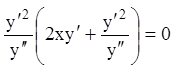 или
или 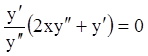 или
или ![]() .
.
О т в е т. Искомое уравнение ![]() .
.
Аналогично дифференциальное уравнение n-го
порядка можно получить, исключая параметры ![]() из n-параметрической
семьи плоских кривых
из n-параметрической
семьи плоских кривых ![]() .
.
Выясним геометрический смысл дифференциального уравнения:
![]() , (1.31)
, (1.31)
рассматривая
переменные ![]() и
и ![]() как
координаты
как
координаты ![]() и
и ![]() двумерной
области Д – области определения функции
двумерной
области Д – области определения функции ![]() .
.
Пусть ![]() является решением
уравнения (1.31). Тогда из геометрического смысла производной, вычисленной в
точке
является решением
уравнения (1.31). Тогда из геометрического смысла производной, вычисленной в
точке ![]() (
(![]() ),
следует, что уравнение (1.31) определяет в каждой точке
),
следует, что уравнение (1.31) определяет в каждой точке ![]() области
Д значение углового коэффициента касательной, проведённой к интегральной кривой
области
Д значение углового коэффициента касательной, проведённой к интегральной кривой
![]() , причём,
, причём, ![]() . Но
если в каждой точке области Д задано значение некоторой величины, то говорят,
что в области Д задано скалярное поле этой величины. Таким образом,
дифференциальное уравнение (1.31) определяет поле направлений касательной
(или просто поле направлений).
. Но
если в каждой точке области Д задано значение некоторой величины, то говорят,
что в области Д задано скалярное поле этой величины. Таким образом,
дифференциальное уравнение (1.31) определяет поле направлений касательной
(или просто поле направлений).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.