Дифференциальные уравнения и математическое моделирование. Основные понятия дифференциальных уравнений. Метод Изоклин, страница 28

Предположим теперь, что семейство кривых (6.42) есть общий интеграл уравнения (6.37). Тогда, если это семейство имеет огибающую, она и будет особым решением данного уравнения.

Действительно, возьмем произвольную точку М(x,y) на огибающей. В этой точке, которая одновременно лежит и на одной из интегральных кривых, направление касательной к огибающей будет совпадать с направлением поля, заданного дифференциальным уравнением (6.37). Следовательно, кривая есть решение данного уравнения. А так как через каждую точку кривой проходят две интегральные кривые – сама кривая l и одна из кривых семейства (6.42), то l есть особое решение.

Установим, как по заданному семейству кривых (6.42) найти огибающую этого семейства. Заметим, что не каждое однопараметрическое семейство кривых имеет огибающую. Например, семейство прямых , семейство концентрических окружностей  огибающей не имеют, тогда как семейство парабол  имеет огибающую . Семейство синусоид имеет даже две огибающие  (рис.26).

Получим необходимые условия существования огибающей. Пусть семейство (6.42) имеет огибающую, уравнение которой запишется параметрически:

,                                                (6.43)

где y(t), x(t) – дифференцируемые функции в области изменения параметра .

Так как огибающая при изменении t касается все новых и новых кривых из семейства (6.42), то величину с в (6.42) будем рассматривать как функцию от t, т.е. . Будем предполагать, что , , так как в противном случае огибающая в каждой своей точке будет касаться одной и той же интегральной кривой из семейства (6.42), а значит она совпадает с этой кривой.

Тогда, подставляя (6.43) в (6.42), получаем тождество:

.

Предполагая теперь, что имеет непрерывные частные производные первого порядка, находим:

.                                          (6.44)

Найдем теперь угловой коэффициент  k касательной к кривой семейства при условии, что . Это будет:

.

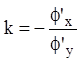Угловой коэффициент k₁ касательной к огибающей равен:

.

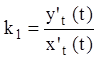Но так как , то  .   Тогда из (6.44) получаем:

.

Итак, если семейство кривых (6.42) имеет огибающую и в каждой точке семейства , или же , то координаты огибающей должны одновременно удовлетворять уравнениям:

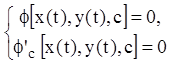.                                                         (6.45)

Полученные уравнения (6.45) являются, таким образом, необходимым условием того, чтобы кривая (6.43) была огибающей семейства (6.42).

Кривая, координаты которой удовлетворяют системе уравнений (6.45), называется с-дискриминантной кривой семейства кривых (6.42) (СДК).

Можно показать, что условия (6.45), если в каждой точке кривой (6.43) одновременно не обращаются в нуль  и  , являются и достаточными для того, чтобы эта кривая была огибающей семейства (6.42).

Таким образом, для нахождения огибающей семейства кривых, зависящих от одного параметра, мы приходим к следующему алгоритму:

из системы уравнений (6.45), путем исключения параметра с, находим с-дискриминантную кривую данного семейства кривых;

из полученной таким образом с-дискриминантной кривой удаляем точки, где одновременно обращаются в нуль  и .

Оставшаяся часть с-дискриминантной кривой и составит огибающую данного семейства кривых.

П р и м е р 7. Найти особое решение уравнения Клеро 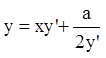 , если общее решение 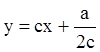, где с –произвольная постоянная, а – параметр.

Р е ш е н и е. Составляем для уравнения Клеро систему уравнений (6.45): 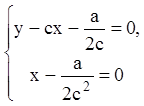  . Из второго уравнения системы находим и подставляем в первое уравнение: .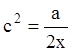

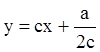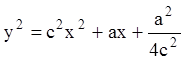
Из первого уравнения  ,           - с-дискриминантная кривая. Из нее удаляем точки, где одновременно обращаются в нуль  и .

.

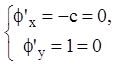Таким образом, кривая  - особое решение – огибающая общего решения.

П р и м е р 8. Найти особое решение уравнения Клеро

.

Р е ш е н и е. Мы получили общее решение уравнения Клеро:

,

где с – константа.

Составляем систему (3.92):

.

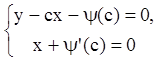Предполагая, что второе уравнение последней системы разрешимо относительно с, получаем , и, подставляя в первое уравнение системы, получим:

 - СДК.

Так как здесь , то построенная СДК и есть огибающая, т.е. особое решение.

Напомним, что мы уже показывали, что функция является решением уравнения Клеро.