Дифференциальные уравнения и математическое моделирование. Основные понятия дифференциальных уравнений. Метод Изоклин, страница 14

Уравнения в полных дифференциалах достаточно легко интегрируются. Поэтому возникает вопрос, нельзя ли каким-то образом в общем случае уравнение (4.1) свести к уравнению в полных дифференциалах? В частности, нельзя ли найти такую функцию , чтобы после умножения на неё левой части равенства (4.1) превратить её в полный дифференциал?

Оказывается, при определённых условиях это можно сделать. При этом множитель  называют интегрирующим множителем уравнения (4.1). Ответ на поставленный вопрос даёт теорема.

Т е о р е м а 2. Если для уравнения (4.1) выполняются условия теоремы 1 и уравнение имеет общий интеграл , то оно имеет бесконечное множество интегрирующих множителей и все они выражаются формулой , где  - произвольная дифференцируемая функция,  - один интегрирующий множитель.

Д о к а з а т е л ь с т в о. 1. Покажем сначала, что при выполнении условий теоремы существует хотя бы один интегрирующий множитель. Предположим, что уравнение (4.1) имеет общий интеграл (4.4) . Запишем уравнение (4.1) и дифференциал его общего интеграла

;

.

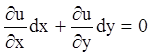Рассматривая эти два равенства как однородную систему алгебраических уравнений относительно ,  и учитывая, что , т. е. система имеет нетривиальное решение, делаем вывод, что её определитель равен нулю

.

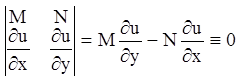Отсюда при  следует равенство

.

Приравнивая эти отношения к , получим 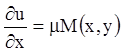, 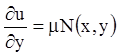. Значит, уравнение (4.1) после умножения его на множитель  сводится к уравнению в полных дифференциалах:

.

Этим доказано существование интегрирующего множителя.

2. Покажем теперь, что интегрирующих множителей бесконечное множество.

Пусть найден один интегрирующий множитель , т. е. , и ему соответствует общий интеграл  уравнения (4.1). Тогда существует бесконечное множество интегрирующих множителей этого уравнения и все они выражаются формулой , где  - произвольная дифференцируемая функция.

Очевидно, что функция , где  - произвольная дифференцируемая функция, тоже будет общим интегралом уравнения. В самом деле, поскольку на интегральных кривых уравнения (4.1) , то на этих самых кривых . Так как

           (4.17)

то  - интеграл уравнения (4.1) и, согласно (4.17),

 -                   (4.18)

его интегрирующий множитель. Из произвольности функции , а значит и  интегрирующих множителей вида (4.18) бесконечное множество.

С л е д с т в и е. Если уравнение (4.1) имеет два независимых интегрирующих множителя  и , то общий интеграл уравнения может быть найден без квадратур в виде

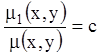.                          (4.19)

В самом деле, из (4.18) следует, что если функция  непрерывно дифференцируемая, то  - интеграл уравнения (4.1), и его общий интеграл определяется равенством (4.19).

З а м е ч а н и е 1. При умножении уравнения (4.1) на интегрирующий множитель  могут появиться посторонние решения, которые появляются из уравнения . Их необходимо найти и отбросить.

П р и м е р  1. Уравнение

имеет независимые интегрирующие множители  и . Построить общее решение.

Р е ш е н и е. Из замечания 1 следует, что  - общий интеграл. Поэтому 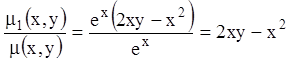 и общий интеграл .

Обратим внимание, что в этом примере после умножения уравнения на  получаем уравнение

,

которое обращается в ноль при , т. е. при  и 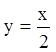. Но это не посторонние решения уравнения, так как они входят в общее решение и являются частными решениями при .

К сожалению, общего простого алгоритма для нахождения интегрирующего множителя нет. Поэтому только в отдельных простейших случаях при помощи искусственных приёмов удаётся из бесконечного их множества найти какой-то один интегрирующий множитель. Например, Лагранж вообще отрицал полезность метода интегрирующего множителя.

Прежде всего, построим уравнение для нахождения интегрирующих множителей. Пусть  является интегрирующим множителем уравнения

,                    (4.1)

тогда:

;

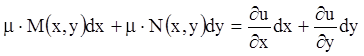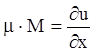 и .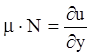

Тогда из равенства смешанных частных производных следует: равенство

;

;

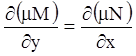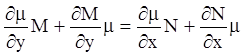.                                   (4.20)