где u и v – вещественные переменные. Тогда уравнение (6.18) запишется:
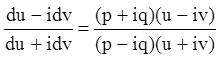 (6.22)
(6.22)
или ![]() .
.
Замечая, что это равенство имеет вид ![]() и, приравнивая к нулю мнимые части,
придем к уравнению
и, приравнивая к нулю мнимые части,
придем к уравнению
![]() .
(6.23)
.
(6.23)
Преобразуем уравнение к виду:
![]()
и делим обе части на ![]() ,
получаем:
,
получаем:
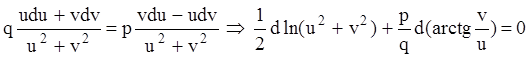 .
.
Проинтегрировав, получаем:
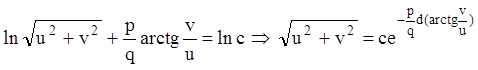 .
.
Вводя на плоскости u,v полярные координаты: ![]() ,
получим:
,
получим:
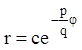 .
(6.24)
.
(6.24)
Это семейство логарифмических спиралей на плоскости u,v. Из формулы (6.24) следует, что
все интегральные кривые уравнения (6.23) примыкают к особой точке (![]() ), при
), при ![]() , если p и q одного знака (см. рис.18) (или
при
, если p и q одного знака (см. рис.18) (или
при ![]() , если p и q противоположных знаков), но не имеют в ней определенного
направления. Все кривые бесконечное число раз обходят особую точку в одном и
том же направлении, асимптотически приближаясь к ней. Та же качественная
картина будет иметь место и в окрестности особой точки
, если p и q противоположных знаков), но не имеют в ней определенного
направления. Все кривые бесконечное число раз обходят особую точку в одном и
том же направлении, асимптотически приближаясь к ней. Та же качественная
картина будет иметь место и в окрестности особой точки ![]() исходного
уравнения (6.4). Такая особая точка называется фокусом.
исходного
уравнения (6.4). Такая особая точка называется фокусом.
Корни ![]() и
и ![]() чисто мнимые
чисто мнимые ![]() .
.
Полагая в (6.24) ![]() ,
получаем:
,
получаем:
![]() .
(6.25)
.
(6.25)
Отсюда следует, что все интегральные кривые уравнения
(6.23) являются окружностями с центром в особой точке ![]() ,
а интегральные кривые уравнения (6.4) – эллипсы, окружающие особую точку
,
а интегральные кривые уравнения (6.4) – эллипсы, окружающие особую точку ![]() . В этом случае особая точка называется центром.
. В этом случае особая точка называется центром.
Итак, в случае различных характеристических чисел мы имеем четыре возможных типа особой точки: узел, седло, фокус и центр.
II. Рассмотрим случай кратных
характеристических чисел уравнения (6.14): 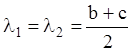 .
Подставляя эти значения в систему (6.12), получаем
.
Подставляя эти значения в систему (6.12), получаем
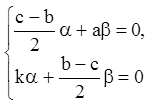 ,
(6.26)
,
(6.26)
причем, определитель этой системы равен нулю по самому
выбору числа ![]() . Поэтому имеем
. Поэтому имеем
![]() (6.27)
(6.27)
Возможны два случая.
Система (6.26) не тождественная, т.е. не все коэффициенты ее равны нулю.
Предположим, что ![]() .
Тогда, положив
.
Тогда, положив ![]() , получим
, получим 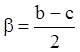 . Сделаем теперь в уравнении (6.4)
подстановку:
. Сделаем теперь в уравнении (6.4)
подстановку:
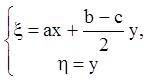 .
(6.28)
.
(6.28)
Тогда будем иметь:
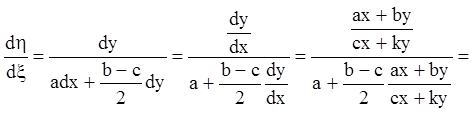
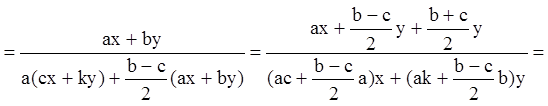
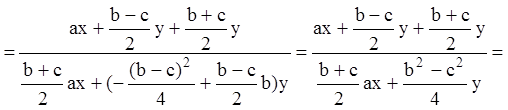
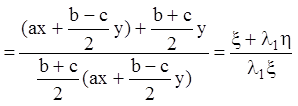 . (6.29)
. (6.29)
Таким образом, преобразование (6.28) приводит уравнение (6.4) к уравнению:
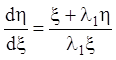 (6.30)
(6.30)
с особой точкой ![]() .
.
Интегрируя последнее уравнение, преобразуем его так:
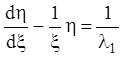 .
.
Рассматривая это уравнение как линейное (оно является и однородным), по общей формуле получаем:
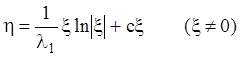 .
(6.31)
.
(6.31)
Все интегральные кривые, определенные формулой (6.31),
примыкают к особой точке ![]() (рис. 20), входя в
нее с одним и тем же направлением (вдоль оси
(рис. 20), входя в
нее с одним и тем же направлением (вдоль оси ![]() ), так
как:
), так
как:
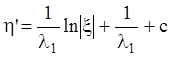 и
и ![]() (6.32)
(6.32)
(знак противоположен знаку ![]() ).
Очевидно, что обе части оси
).
Очевидно, что обе части оси ![]() также являются
интегральными кривыми, входящими в особую точку
также являются
интегральными кривыми, входящими в особую точку ![]() с тем
же направлением, что и интегральные кривые (6.31). Следовательно, в
рассматриваемом случае особая точка
с тем
же направлением, что и интегральные кривые (6.31). Следовательно, в
рассматриваемом случае особая точка ![]() уравнения (6.30) и
соответственно особая точка
уравнения (6.30) и
соответственно особая точка ![]() уравнения (6.4)
называется вырожденным узлом. В вырожденном узле все интегральные кривые
примыкают к особой точке с одним и тем же направлением, в то время, как в
случае обыкновенного узла две интегральные кривые уравнения (а именно полуоси
оси
уравнения (6.4)
называется вырожденным узлом. В вырожденном узле все интегральные кривые
примыкают к особой точке с одним и тем же направлением, в то время, как в
случае обыкновенного узла две интегральные кривые уравнения (а именно полуоси
оси ![]() ) примыкали к особой точке с направлением,
отличным от направления всех других интегральных кривых.
) примыкали к особой точке с направлением,
отличным от направления всех других интегральных кривых.
Система (6.26) тождественная.
В этом случае ![]() . Тогда уравнение
(6.4) принимает вид:
. Тогда уравнение
(6.4) принимает вид:
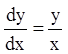 .
(6.33)
.
(6.33)
Его решение:
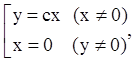 (6.34)
(6.34)
Все они примыкают к особой точке ![]() с
определенным (своим для каждой кривой) направлением. Такая особая точка
называется (особым) дикритическим узлом.
с
определенным (своим для каждой кривой) направлением. Такая особая точка
называется (особым) дикритическим узлом.
Суммируя полученные выше результаты, делаем вывод, что для
дифференциального уравнения (6.4) точка (0,0) является особой. Тип особенности
определяется корнями или, что одно и то же, дискриминантом характеристического
уравнения (6.14), т.е. числом ![]() . А именно:
. А именно:
![]() , если
, если
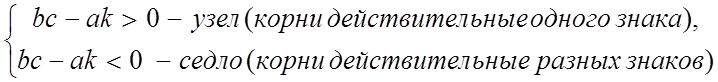 ;
;
![]() , если
, если
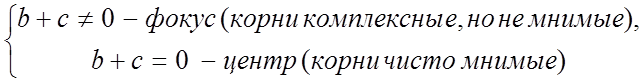 ;
;
![]() , если
, если
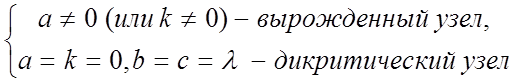
П р и м е р 1. Исследовать поведение интегральных кривых
уравнения 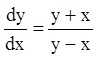 в окрестности точки (0,0).
в окрестности точки (0,0).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.