2.3 Однородные дифференциальные уравнения
2.4 Уравнения, сводящиеся к однородным
В общем случае дифференциальное уравнение I-го порядка можно записать в виде
![]() , (2.1)
, (2.1)
или в виде разрешенном относительно производной
![]() ,
(2.2)
,
(2.2)
или в симметричной форме:
![]() ,
(2.3)
,
(2.3)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() - заданные функции своих аргументов.
- заданные функции своих аргументов.
Для дифференциального уравнения I-го порядка имеют место введённые ранее понятия решения, общего и частного решения, общего и частного интегралов.
С геометрической точки зрения общее решение
дифференциального уравнения I-го порядка ![]() представляет собой
однопараметрическое семейство интегральных кривых. Частное решение –
единственная кривая из однопараметрического семейства
представляет собой
однопараметрическое семейство интегральных кривых. Частное решение –
единственная кривая из однопараметрического семейства ![]() ,
соответствующая конкретному значению параметра
,
соответствующая конкретному значению параметра ![]() .
Например, общим решением дифференциального уравнения
.
Например, общим решением дифференциального уравнения ![]() является
однопараметрическое семейство парабол
является
однопараметрическое семейство парабол ![]() .
Положив в общем решении, например,
.
Положив в общем решении, например, ![]() , получим частное
решение – единственную интегральную кривую
, получим частное
решение – единственную интегральную кривую ![]() .
.
Задачей Коши для дифференциального уравнения I-го порядка называют задачу нахождения частного решения, удовлетворяющего заданному начальному условию:
![]() ,
(2.4)
,
(2.4)
где ![]() ,
, ![]() -
заданные числа. С геометрической точки зрения решить задачу Коши для
дифференциального уравнения I-го порядка значит из однопараметрического семейства
интегральных кривых (общего решения) выбрать единственную интегральную кривую,
проходящую через заданную точку
-
заданные числа. С геометрической точки зрения решить задачу Коши для
дифференциального уравнения I-го порядка значит из однопараметрического семейства
интегральных кривых (общего решения) выбрать единственную интегральную кривую,
проходящую через заданную точку ![]() .
.
П р и м е р 1. Проверить, что функция ![]() является общим решением уравнения
является общим решением уравнения ![]() , и найти частное решение, удовлетворяющее
начальному условию
, и найти частное решение, удовлетворяющее
начальному условию ![]() .
.
Р е ш е н и е. Из ![]() вычисляем
вычисляем
![]() и, подставляя в уравнение, получаем
и, подставляя в уравнение, получаем ![]() . Таким образом,
. Таким образом, ![]() общее
решение уравнения, геометрический смысл – однопараметрическое семейство
интегральных кривых. Из начальных условий получаем
общее
решение уравнения, геометрический смысл – однопараметрическое семейство
интегральных кривых. Из начальных условий получаем ![]() .
Подставив в общее решение значение
.
Подставив в общее решение значение ![]() получим,
получим, ![]() .
.
О т в е т: ![]() .
.
а) Неполные уравнения первого порядка.
I.
![]() . (2.7)
. (2.7)
непосредственным интегрированием
находим 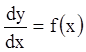 ,
, ![]() ,
, ![]() .
.
II.
![]() (2.8)
(2.8)
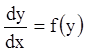 .
Считая
.
Считая ![]() функцией, а
функцией, а ![]() аргументом
и полагая
аргументом
и полагая ![]() , получаем
, получаем 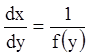 ;
; 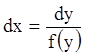 ;
; 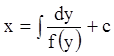 -
общее решение.
-
общее решение.
П р и м е р 1. ![]() ,
, ![]() .
.
П р и м е р 2. ![]() ;
; 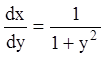 ;
;
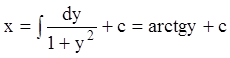 - общее решение.
- общее решение.
б) Уравнением с разделёнными переменными называют уравнение вида
![]() , (2.9)
, (2.9)
в котором ![]() и
и ![]() - заданные функции. Общий интеграл
находим, интегрируя уравнение
- заданные функции. Общий интеграл
находим, интегрируя уравнение ![]() , где
, где ![]() - произвольная постоянная.
- произвольная постоянная.
П р и м е р 3. Найти частное решение дифференциального
уравнения ![]() , удовлетворяющее условию
, удовлетворяющее условию ![]() .
.
Р е ш е н и е. ![]() или
или 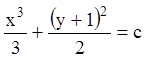 - общий интеграл. Используя начальные
условия, получаем
- общий интеграл. Используя начальные
условия, получаем 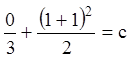 , откуда
, откуда ![]() .
Частное решение -
.
Частное решение - 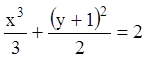 .
.
в) Дифференциальное уравнение вида:
![]() , (2.10)
, (2.10)
в котором
коэффициенты при ![]() и
и ![]() представляют
произведение двух функций из которых одна зависит только от
представляют
произведение двух функций из которых одна зависит только от ![]() , а другая только от
, а другая только от ![]() , называют уравнением с разделяющимися
переменными.
, называют уравнением с разделяющимися
переменными.
Полагая, что
![]() (2.11)
(2.11)
и разделив уравнение (2.10) на
произведение (2.11), получим уравнение с разделёнными переменными 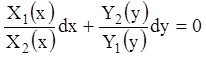 . Проинтегрировав его, получим
. Проинтегрировав его, получим 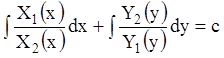 - общий интеграл уравнения.
- общий интеграл уравнения.
З а м е ч а н и е 1. Иногда для разделения переменных
вводят разделяющий множитель 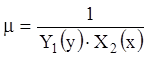 . Умножив уравнение
(2.10) на
. Умножив уравнение
(2.10) на ![]() , получим уравнение с разделёнными
переменными.
, получим уравнение с разделёнными
переменными.
З а м е ч а н и е 2. Деление на ![]() может привести к потере частных решений,
обращающих в ноль это произведение (эти решения могут быть и особыми).
может привести к потере частных решений,
обращающих в ноль это произведение (эти решения могут быть и особыми).
З а м е ч а н и е 3. Уравнение вида
![]() (2.12)
(2.12)
тоже является уравнением с разделяющимися переменными и легко приводится к уравнению (2.10):
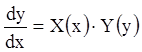 ;
; ![]() - вид (2.10).
- вид (2.10).
Полагая ![]() , получим
, получим 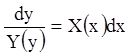 и
и 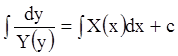 -
общий интеграл.
-
общий интеграл.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.