Заметим, что, полагая ![]() , мы
могли потерять решения
, мы
могли потерять решения ![]() , где
, где ![]() -
действительные корни уравнения
-
действительные корни уравнения ![]() . Поэтому этот случай
следует рассмотреть отдельно. Если окажется, что уравнение
. Поэтому этот случай
следует рассмотреть отдельно. Если окажется, что уравнение ![]() имеет действительные корни
имеет действительные корни ![]() , которые, следовательно, будут решениями
уравнения (5.79) и эти решения не содержатся в общем интеграле (5.82), то они
могут оказаться особыми решениями уравнения (5.79).
, которые, следовательно, будут решениями
уравнения (5.79) и эти решения не содержатся в общем интеграле (5.82), то они
могут оказаться особыми решениями уравнения (5.79).
П р и м е р 7. Решить уравнение:
![]() .
.
Р е ш е н и е. Это уравнение вида IV(2),
т.к. ![]() .
.
Пусть![]() и
и ![]() в силу (5.82). Тогда из (5.82)
в силу (5.82). Тогда из (5.82)
 .
.
И общее решение в параметрической форме:
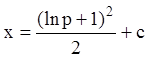 ,
, ![]() .
.
П р и м е р 8. Решить уравнение:
![]() .
.
Р е ш е н и е. Это уравнение разрешимо относительно y, поэтому:
 ,
, 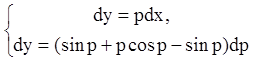 .
.
![]() ,
, ![]() или
или ![]() .
.
 .
. ![]() ,
,
где ![]() - нули уравнения.
- нули уравнения. ![]()
![]() - особое решение.
- особое решение.
Рассмотрим уравнение (5.7)
![]() ,
,
полагая ![]() , где z
– аппликата некоторой пространственной точки М, как
, где z
– аппликата некоторой пространственной точки М, как ![]() , т.е.
как уравнение некоторой поверхности S. Но уравнение
поверхности S иногда удается записать параметрически:
, т.е.
как уравнение некоторой поверхности S. Но уравнение
поверхности S иногда удается записать параметрически:
![]() , (5.83)
, (5.83)
где u и v – параметры, так что:
![]() .
.
Предполагая, что функции ![]() и
и ![]() в области изменения параметров u и v дифференцируемые, имеем:
в области изменения параметров u и v дифференцируемые, имеем:
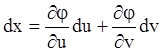 ,
, 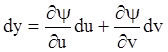 ,
,
откуда, учитывая, что 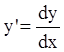 ( и
( и
![]() ) , получаем уравнение:
) , получаем уравнение:
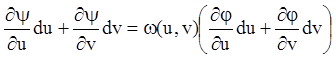 , (5.84)
, (5.84)
связывающее между собой параметры u
и v. Принимая в (5.84) v за
независимую переменную, u за искомую функцию, группируя
члены с du и dv и предполагая,
что 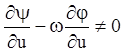 , получаем
, получаем
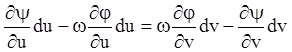
или:
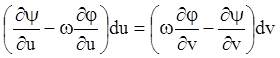 .
.
Отсюда получаем уравнение, разрешенное относительно производной:
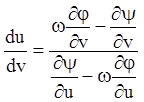 (5.85)
(5.85)
с непрерывной правой частью. Если данное уравнение
интегрируется, то его общее решение ![]() в совокупности с
уравнениями
в совокупности с
уравнениями ![]() дает общее решение
дает общее решение
![]() (5.86)
(5.86)
исходного уравнения (5.7) в параметрической форме (здесь v – параметр, с – произвольная постоянная).
З а м е ч а н и е. Изложенный метод решения уравнения (5.7) возможен, если: 1) уравнение (5.7) допускает параметризацию; 2) полученное уравнение (5.85) интегрируется.
В частности, например, если уравнение (5.7) можно
разрешить относительно y: ![]() , то
за параметры u и v можно взять x и y', положив
, то
за параметры u и v можно взять x и y', положив ![]() . Получим
. Получим ![]() .
Следовательно, если уравнение (5.85), которое в данном случае запишется:
.
Следовательно, если уравнение (5.85), которое в данном случае запишется:
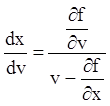 ,
,
интегрируется, то будет интегрироваться и исходное уравнение.
Например, если уравнение ![]() разрешимо
относительно х, т.е.
разрешимо
относительно х, т.е. ![]() , то
, то 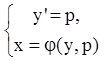 -
параметрическое представление уравнения.
-
параметрическое представление уравнения. ![]() из
первого уравнения,
из
первого уравнения, 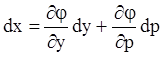 из второго. Тогда,
из второго. Тогда, 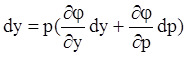 . Разделив на
. Разделив на ![]() и на
и на ![]() , получим:
, получим:  .
Предположим, что последнее уравнение имеет решение
.
Предположим, что последнее уравнение имеет решение ![]() .
Тогда, общий интеграл исходного уравнения запишется:
.
Тогда, общий интеграл исходного уравнения запишется: ![]()
П р и м е р 9. В качестве примера на изложенную в п. V теорию рассмотрим уравнение Лагранжа:
![]() (5.87)
(5.87)
где ![]() - непрерывно
дифференцируемые функции.
- непрерывно
дифференцируемые функции.
Р е ш е н и е. Положим ![]() ,
тогда (5.87) запишется:
,
тогда (5.87) запишется:
![]() (5.88)
(5.88)
Дифференцируя (5.88) и принимая во внимание, что ![]() , получаем:
, получаем:
![]() ,
,
откуда:
 ,
,
или, полагая ![]() , получаем:
, получаем:
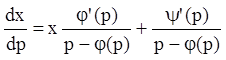 или
или 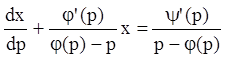 .
(5.89)
.
(5.89)
Уравнение (5.89) – линейное. Его решение находится при помощи двух квадратур и имеет вид:
![]() .
.
Тогда общее решение уравнения (5.87) в параметрической форме запишется:
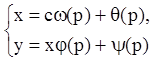 (5.90)
(5.90)
Если возможно, исключают параметр p и получают непосредственную зависимость между x и y.
З а м е ч а н и е 1. Выполняя операцию деления на ![]() , можно потерять некоторые решения, а
именно те, для которых
, можно потерять некоторые решения, а
именно те, для которых ![]() , т.е. решения
, т.е. решения ![]() . Если уравнение
. Если уравнение ![]() имеет
указанные действительные корни, то
имеет
указанные действительные корни, то ![]() будет решением
уравнения
будет решением
уравнения  , а прямые:
, а прямые:
![]()
решениями уравнения (5.87). Причем, эти решения не содержатся в общем решении (5.90) и являются особыми.
З а м е ч а н и е 2. Уравнение (5.87) в литературе связывают с именем Лагранжа, хотя вернее было бы назвать его уравнением Даламбера, который впервые (1750 г.) нашел его общее и особое решения. Лагранж же впервые (в 1774 г.) дал геометрическое толкование особых решений уравнения как огибающих семьи интегральных кривых.
П р и м е р 10. Проинтегрировать уравнение:
![]() .
.
Р е ш е н и е. Сравнив с (5.87) убеждаемся, что это
уравнение Лагранжа, в котором ![]() . Поэтому положим
. Поэтому положим ![]() . Тогда
. Тогда ![]() .
Дифференцируя, находим:
.
Дифференцируя, находим:
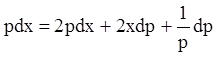 , откуда
, откуда 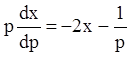 или
или
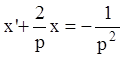 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.