Дифференциальные уравнения и математическое моделирование. Основные понятия дифференциальных уравнений. Метод Изоклин, страница 31

Функция  называется особым решением дифференциального уравнения (7.2), если:

1)  обращает уравнение (7.2) в тождество;

2)  для любой точки задача Коши с начальными условиями   имеет более чем одно решение.

Соотношение вида:

,        (7.12)

(где y – решение уравнения (7.1)), получаемое при интегрировании уравнения (7.1), называется промежуточным интегралом k-го порядка уравнения (7.1). Знание промежуточного интеграла k-го порядка (7.12) позволяет свести задачу интегрирования уравнения n-го порядка к более простой задаче интегрирования уравнения (n-k)-го порядка. Промежуточный интеграл:

                                          (7.13)

называется первым интегралом.

7.2 Некоторые типы уравнений n-го порядка, интегрируемые в квадратурах

Дифференциальное уравнение n-го порядка проинтегрировать удается только в очень редких случаях. Рассмотрим эти случаи:

I.  Уравнение вида

,                                                       (7.14)

которое удается разрешить относительно или относительно  или, наконец,  и , можно выразить через какой-то параметр.

1)  Пусть уравнение (7.14) можно разрешить относительно , т.е.

.                                                         (7.15)

Его всегда можно проинтегрировать. По определению

.

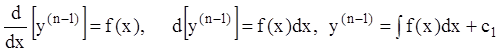Аналогично

,

………………………………………………………………

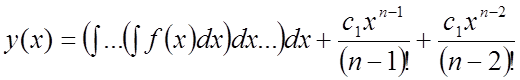
.                                                                                                                      (7.16)

Частное решение уравнения (7.15), удовлетворяющее начальным условиям (7.3), находим так же:

,

,

……………………………………………………………………………

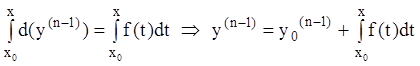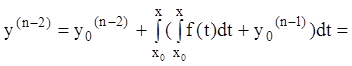
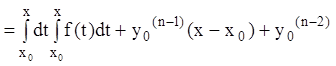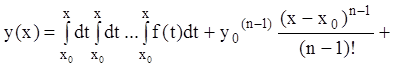
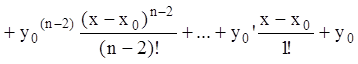.              (7.17)

Формула (7.17) содержит n квадратур, однако их можно заменить одной, а именно, можно показать, что имеет место формула Коши:

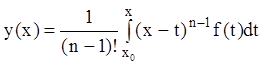.                                 (7.18)

Для доказательства формулы (7.18) разложим функцию  по формуле Тейлора, а остаточный член запишем в виде интеграла:

,

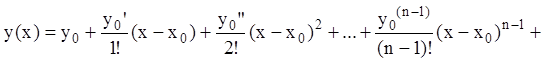
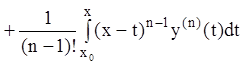где - значения функции  и ее производных при .

Полагая начальные условия  и учитывая, что  (7.15),  из последней формулы  находим:

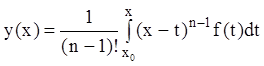.                                 (7.19)

Формула (7.19) дает решения уравнения (7.15) при нулевых начальных условиях, но то же решение уравнения (7.15) дает и n-кратная квадратура 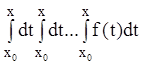, поэтому

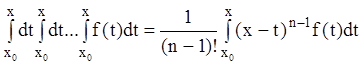,                             (7.20)

так как в нашем случае .

Тогда, в силу (7.20) формула (7.17) запишется:

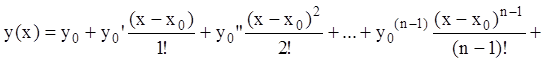
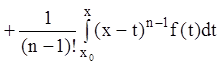.                                                                                                                                                                                                                                                                 (7.21)

П р и м е р 1. Найти частное и общее решение уравнения , если , где  - любые числа.

Р е ш е н и е. По формуле (7.21) будем иметь:

.

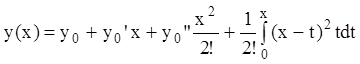Вычисляем отдельно:

,

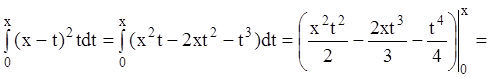
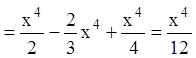поэтому окончательно 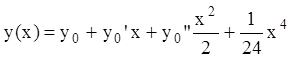 - частное решение.

Учитывая, что  - произвольные числа, поэтому зависимость 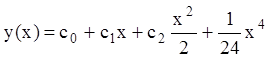 - общее решение.

2)  Пусть уравнение (7.14) можно разрешить относительно x, т.е.:

.                          (7.22)

Положим: . Тогда из (7.22) следует:  и  . Так как . Откуда: . Аналогично:

  и

………………………………………………………………

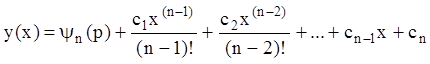 ,                           (7.23)

что вместе с  дает общее решение дифференциального уравнения (7.22) в параметрической форме.

П р и м е р 2. Найти решение уравнения .

Р е ш е н и е. Из условия . Положив , то

.

Т.к.

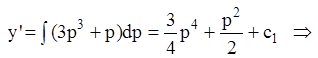
т.к. 

.

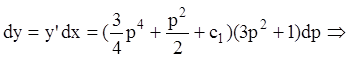
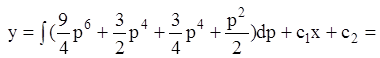
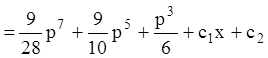Тогда общее решение в параметрической форме:

.

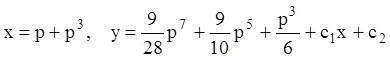3)  Пусть уравнение (7.14) нельзя разрешить ни относительно x, ни относительно , но можно выразить x и  как функции параметра t, т.е.:

                (7.24)

равносильные уравнению (7.14). И в этом случае уравнение интегрируется в квадратурах. Действительно, с учетом (7.14) , или . Аналогично  и

  и т.д.

Решение в параметрической форме запишется:

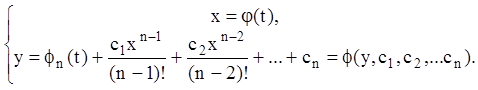     (7.25)

П р и м е р 3. Решить уравнение .

Р е ш е н и е. Пусть , тогда .

Так как:

. 

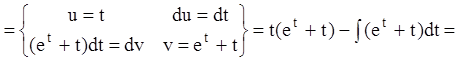
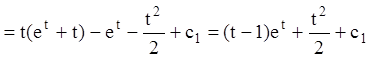Так как:

  

.

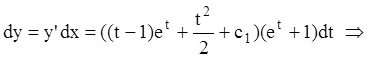
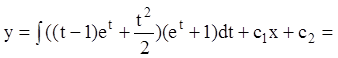
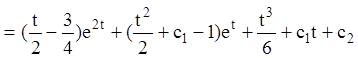Тогда общее решение:

.

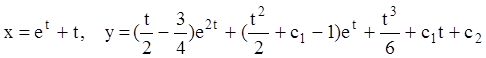II.  Уравнение вида:

.                   (7.26)

Сделаем замену , тогда

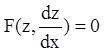,                         (7.27)