Дифференциальные уравнения и математическое моделирование. Основные понятия дифференциальных уравнений. Метод Изоклин, страница 2

Геометрическая теория дифференциальных уравнений изучает связь теории дифференциальных уравнений с теорией поверхностей и пространственных кривых.

Мы будем рассматривать классическую теорию интегрирования дифференциальных уравнений, а также некоторые разделы качественной теории дифференциальных уравнений, в частности, теорию устойчивости А.М. Ляпунова.

1.2 Основные понятия дифференциальных уравнений

Дифференциальным уравнением называют уравнение, связывающее независимую переменную , искомую функцию  и её производные или дифференциалы. Дифференциальное уравнение называется обыкновенным, если искомые функции зависят только от одного аргумента, и в частных производных, если неизвестные функции зависят от нескольких переменных. Порядком дифференциального уравнения называют порядок наивысшей производной (или дифференциала), входящих в это уравнение. Если дифференциальное уравнение представлено в виде полинома от производных, то степень его наибольшей производной называют степенью дифференциального уравнения.

Например:

1)  - обыкновенное дифференциальное уравнение 1-го порядка 1-й степени;

2)  - обыкновенное дифференциальное уравнение 1-го порядка 4-й степени;

3) 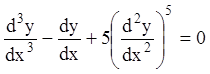 - обыкновенное дифференциальное уравнение 3-го порядка 1-й степени;

4)  - обыкновенное дифференциальное уравнение 1-го порядка 1-й степени;

5)  - обыкновенное дифференциальное уравнение 2-го порядка 1-й степени;

6) 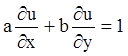 - дифференциальное уравнение в частных производных 1-го порядка;

7) 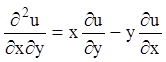 - дифференциальное уравнение в частных производных 2-го порядка;

Общий вид обыкновенного дифференциального уравнения n-го порядка:

          ,                                      (1.1)

где  - некоторая заданная функция.

Решением дифференциального уравнения n-го порядка на интервале  называется функция , определённая на  вместе со своими производными до n-го порядка включительно, и такая, что её подстановка в дифференциальное уравнение превращает последнее в тождество по  на , т. е.:

, .

П р и м е р 1. Показать, что функция  является решением уравнения  на .

Р е ш е н и е. Вычисляем : ,

 . Подставляем  и  в уравнение

  ч.т.д.

Процесс нахождения решений называется интегрированием дифференциальных уравнений. График решения дифференциального уравнения называется интегральной кривой этого уравнения.

Общим решением дифференциального уравнения n-го порядка называют функцию вида:

          ,                          (1.2)

которая является решением этого уравнения и содержит столько произвольных постоянных , каков порядок этого уравнения. Эту же функцию, но записанную в неявном виде,

                                                      (1.3)

называют общим интегралом дифференциального уравнения (1.1).

Частным решением дифференциального уравнения называют решение, получаемое из общего решения (1.2) при конкретном выборе значений произвольных постоянных .

Задачей Коши для некоторого дифференциального уравнения называют задачу нахождения частного решения этого уравнения, удовлетворяющего заданным начальным условиям.

Соотношение, полученное из общего интеграла (1.3) при конкретных значениях произвольных постоянных , называют частным интегралом дифференциального уравнения (1.1).

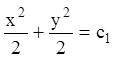П р и м е р 2. Решить дифференциальное уравнение . Интегрируем   или  () – общий интеграл уравнения. Общее решение - . Положив, например,  получим частный интеграл  и частное решение .

1.3 О решении прикладных задач на составление дифференциальных уравнений

Вопрос составления дифференциальных уравнений по условию задачи состоит в нахождении зависимости между переменными величинами и их приращениями. При этом важное и подчас главенствующее значение имеет знание законов той области науки с которой связана природа изучаемой задачи. Так, например, в механике это могут быть законы Ньютона, в теории электрических цепей – законы Кирхгофа и т.д. Универсального метода составления дифференциальных уравнений, пригодного во всех случаях, указать нельзя. Можно дать лишь некоторые общие рекомендации. В большинстве случаев методика решения прикладных задач на составление дифференциальных уравнений сводится к следующему: