З а м е ч а н и е 4. В 1694-97 гг. Иоган Бернулли разработал метод “разделения переменных”.
П р и м е р 4. Найти частное решение дифференциального
уравнения ![]() , если
, если ![]() .
.
Р е ш е н и е. 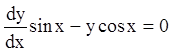 умножив
на
умножив
на ![]() , получим
, получим ![]() - это
уравнение вида (2.10). Полагая
- это
уравнение вида (2.10). Полагая ![]() , получаем
, получаем 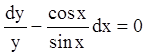 ;
; 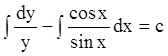 или
или ![]() или
или ![]() - общее
решение. Используя начальные условия, получаем
- общее
решение. Используя начальные условия, получаем 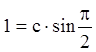 ,
откуда
,
откуда ![]() . Искомое частное решение
. Искомое частное решение ![]() .
.
г) Уравнение вида:
![]() , (2.13)
, (2.13)
где ![]() ,
, ![]() ,
, ![]() -
заданные постоянные величины, сводится к уравнению с разделяющимися переменными
заменой:
-
заданные постоянные величины, сводится к уравнению с разделяющимися переменными
заменой:
![]() .
(2.14)
.
(2.14)
Действительно, из (2.14) находим 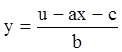 , откуда
, откуда 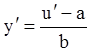 и
уравнение (2.13) запишется
и
уравнение (2.13) запишется
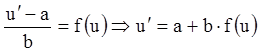 .
.
Полагая ![]() , получаем
, получаем
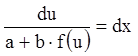 ,
, 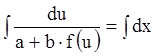 .
.
Вычислив интегралы, получим общий интеграл ![]() . Учитывая замену, получаем
. Учитывая замену, получаем ![]() - общий интеграл.
- общий интеграл.
П р и м е р 5. Найти общий интеграл уравнения ![]() .
.
Р е ш е н и е. Это уравнение вида (2.13). Полагая ![]() , находим
, находим ![]() , откуда
, откуда
![]() . Подставляем в уравнение
. Подставляем в уравнение ![]() - это уравнение с разделяющимися
переменными:
- это уравнение с разделяющимися
переменными: 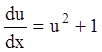 ;
; 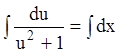 (
(![]() )
) ![]() или
или ![]() - общий интеграл.
- общий интеграл.
Функция ![]() называется однородной
функцией своих аргументов измерения
называется однородной
функцией своих аргументов измерения ![]() , если справедливо
тождество
, если справедливо
тождество
![]() . (2.15)
. (2.15)
Например, функция ![]() есть
однородная функция второго измерения, так как
есть
однородная функция второго измерения, так как
![]() .
.
При ![]() имеем функцию нулевого
измерения. Например,
имеем функцию нулевого
измерения. Например, 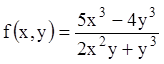 есть однородная функция первого
измерения, так как:
есть однородная функция первого
измерения, так как:
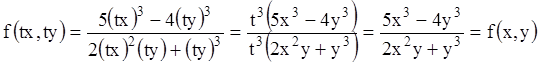 .
.
Уравнения вида
![]() , (2.16)
, (2.16)
в которых правая часть (функция ![]() ) является однородной функцией нулевого
измерения называют однородным относительно
) является однородной функцией нулевого
измерения называют однородным относительно ![]() и
и ![]() . Например, однородными являются уравнения
. Например, однородными являются уравнения 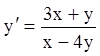 ;
; 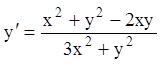 , так
как их правые части являются однородными функциями нулевого измерения.
, так
как их правые части являются однородными функциями нулевого измерения.
Покажем, что однородные уравнения сводятся к уравнениям с разделяющимися переменными.
Пусть для уравнения (2.16) выполняется условие ![]() . Тогда, положив
. Тогда, положив 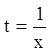 ,
получим равенство:
,
получим равенство:
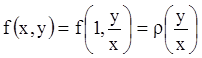
и таким образом делаем вывод, что в
однородных уравнениях (2.16) правая часть фактически является функцией от переменной
![]() .
.
Вводим замену 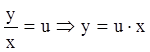 .
Тогда
.
Тогда ![]() и однородное уравнение (2.16) запишется
и однородное уравнение (2.16) запишется ![]() или
или ![]() . Это
уравнение с разделяющимися переменными. Разделяя переменные, получаем
. Это
уравнение с разделяющимися переменными. Разделяя переменные, получаем 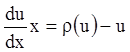 ,
, 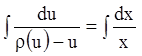 .
Интегрируя, получаем
.
Интегрируя, получаем ![]() . Учитывая замену
. Учитывая замену 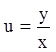 , получаем общий интеграл однородного
уравнения
, получаем общий интеграл однородного
уравнения 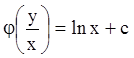 . Если
. Если ![]() , то уравнение
может иметь ещё решения (может, особые).
, то уравнение
может иметь ещё решения (может, особые).
П р и м е р 1. Найти общий интеграл уравнения ![]() .
.
Р е ш е н и е. 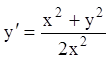 ,
функция
,
функция 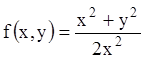 однородная нулевого измерения. Представим
уравнение в виде
однородная нулевого измерения. Представим
уравнение в виде 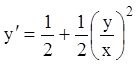 . Замена
. Замена 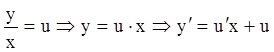 .
Представляем:
.
Представляем: 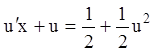 ;
; 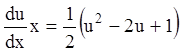 ;
; 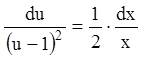 ;
; 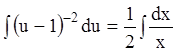 ;
; 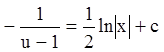 . Так как
. Так как 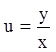 , то
, то 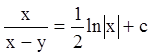 - общий интеграл. При делении на
- общий интеграл. При делении на ![]() потеряно решение
потеряно решение ![]() ,
,
![]() .
.
О т в е т: 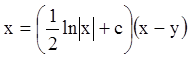 ,
, ![]() .
.
З а м е ч а н и е 1. Уравнение вида
![]() , (2.17)
, (2.17)
в котором
функции ![]() и
и ![]() являются
однородными функциями одного и того же измерения, тоже является однородным. Его
легко преобразовать к виду (2.16)
являются
однородными функциями одного и того же измерения, тоже является однородным. Его
легко преобразовать к виду (2.16) ![]() . Положив
. Положив ![]() , получаем
, получаем 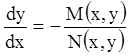 или
или ![]() , где функция
, где функция 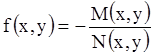 является
однородной функцией нулевого измерения. В самом деле,
является
однородной функцией нулевого измерения. В самом деле, 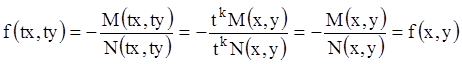 .
.
З а м е ч а н и е 2. В 1694 г. Иоган Бернулли разработал метод сведения однородных уравнений к уравнениям с разделяющимися переменными.
П р и м е р 2. Проинтегрировать уравнение:
![]()
Р е ш е н и е. ![]() ;
; 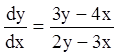 ;
; 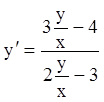 замена
замена
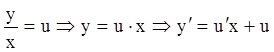 . Подставляя в уравнение
. Подставляя в уравнение 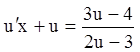 ;
; 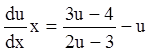 ;
; 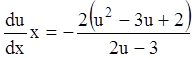 ;
; 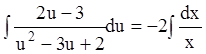 ;
; ![]() ;
; 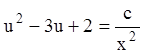 ; так
как
; так
как 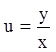 , то
, то 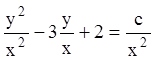 ;
; ![]() - общий интеграл уравнения.
- общий интеграл уравнения.
О т в е т: ![]() .
.
З а м е ч а н и е 3. При решении однородных уравнений
необязательно приводить их к виду 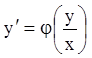 . Можно сразу делать
подстановку
. Можно сразу делать
подстановку ![]() .
.
П р и м е р 3. Решить уравнение ![]() .
.
Р е ш е н и е. Это однородное уравнение, так как его
можно записать в виде 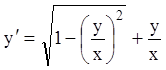 , где правая часть –
однородная функция нулевого измерения. Тогда замена
, где правая часть –
однородная функция нулевого измерения. Тогда замена ![]() .
Подставляя в уравнение выражение для
.
Подставляя в уравнение выражение для ![]() и
и ![]() , получаем
, получаем ![]() .
Сокращая на
.
Сокращая на ![]() , получаем
, получаем 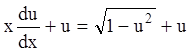 .
Разделяем переменные
.
Разделяем переменные 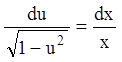 . Интегрируя, находим
. Интегрируя, находим 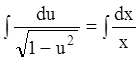 ;
; ![]() или
или ![]() или
или 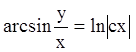 ;
; 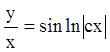 ;
; ![]() .
.
При делении на произведение ![]() могли
потерять решение, обращающее в ноль это произведение. Проверим, не будут ли
решениями
могли
потерять решение, обращающее в ноль это произведение. Проверим, не будут ли
решениями ![]() и
и 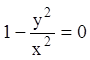 , то
есть
, то
есть ![]() . Находим, что функция
. Находим, что функция ![]() также является решением этого уравнения.
также является решением этого уравнения.
О т в е т: ![]() ,
, ![]() .
.
Уравнения, которые при помощи определённой замены переменных приводятся к однородным, называют обобщённо-однородными.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.