Под знаком интеграла стоит непрерывная функция по ![]() , так как
, так как ![]() -
дифференцируемая а, значит, непрерывная. Соотношения вида (5.3), в которых
неизвестная функция входит под знак интеграла, называют интегральными
уравнениями. Из равенства (5.3) следует, что любое решение уравнения (5.1),
удовлетворяющее условию (5.2), удовлетворяет условию (5.3). Справедливо и
обратное утверждение, т. е. если некоторая функция
-
дифференцируемая а, значит, непрерывная. Соотношения вида (5.3), в которых
неизвестная функция входит под знак интеграла, называют интегральными
уравнениями. Из равенства (5.3) следует, что любое решение уравнения (5.1),
удовлетворяющее условию (5.2), удовлетворяет условию (5.3). Справедливо и
обратное утверждение, т. е. если некоторая функция ![]() при
подстановке в (5.3) обращает его в тождество, то она, очевидно, удовлетворяет
условию (5.2), а дифференцируя тождество (5.3), получим, что
при
подстановке в (5.3) обращает его в тождество, то она, очевидно, удовлетворяет
условию (5.2), а дифференцируя тождество (5.3), получим, что ![]() обращает в тождество и уравнение (5.1).
обращает в тождество и уравнение (5.1).
Таким образом, эквивалентность уравнения (5.1) при начальных условиях (5.2) интегральному уравнению (5.3) установлена. Докажем существование решения уравнения (5.3). С этой целью применим метод последовательных приближений Пикара.
За исходное (нулевое) приближение ![]() принимаем функцию, равную тождественно
начальному значению исходной функции
принимаем функцию, равную тождественно
начальному значению исходной функции ![]() .
.
I. Построим последовательность функций, называемых приближенными решениями, по правилу:
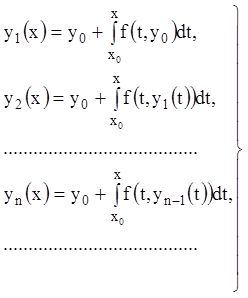 (5.4)
(5.4)
Будем рассматривать функцию (5.4) для ![]() , находящихся в интервале
, находящихся в интервале ![]() . Тогда относительно функций (5.4) можно
утверждать:
. Тогда относительно функций (5.4) можно
утверждать:
1) Каждая из функций ![]() (
(![]() ) непрерывна, так как по условию
теоремы
) непрерывна, так как по условию
теоремы ![]() - непрерывная функция и тогда интеграл
- непрерывная функция и тогда интеграл 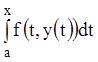 есть непрерывная функция верхнего предела.
есть непрерывная функция верхнего предела.
2) Каждая из функций ![]() (
(![]() ) определена при
) определена при ![]() и не выходит из области
и не выходит из области ![]() . Докажем это. Из соотношений (5.4) имеем:
. Докажем это. Из соотношений (5.4) имеем:
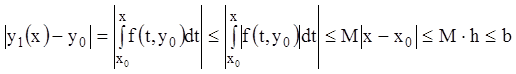 ,
,
так как ![]() -
меньшее из чисел
-
меньшее из чисел ![]() и
и ![]() . Таким
образом, функция
. Таким
образом, функция ![]() не выходит за пределы области
не выходит за пределы области ![]() . Аналогично:
. Аналогично:
 ,
,
…………………………………………………………………………………
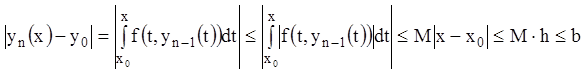 ,
,
…………………………………………………………………………………
Применяя метод индукции, получаем что функции ![]() (
(![]() ) не
выходят из области
) не
выходят из области ![]() .
.
II.
Покажем, что последовательность приближений (5.4) сходится равномерно
при ![]() . Для этого рассмотрим функциональный ряд, k-я
частная сумма которого равна
. Для этого рассмотрим функциональный ряд, k-я
частная сумма которого равна ![]() :
:
![]() . (5.5)
. (5.5)
Из равномерной сходимости этого ряда будет следовать равномерная сходимость последовательности приближений (5.4). Оценим каждый член ряда (5.5):
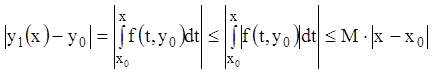 ,
,
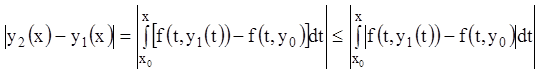 .
.
Применяя к ![]() условие Липшица и
учитывая оценку предыдущего члена ряда, получим:
условие Липшица и
учитывая оценку предыдущего члена ряда, получим:
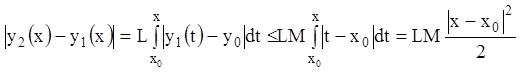 .
.
Аналогично:
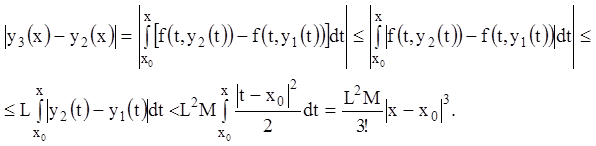
Пользуясь методом математической индукции, нетрудно показать, что:
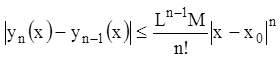 .
(5.6)
.
(5.6)
Если рассматривать ![]() из интервала
из интервала ![]() , то:
, то:
![]() ,
,
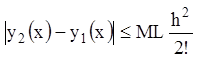 ,
,
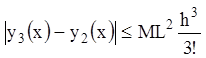 ,
,
……………………………….
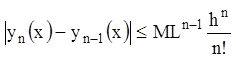 ,
,
……………………………….
Таким образом, члены функционального ряда (5.5) меньше соответствующих членов числового ряда с положительными членами:

Последний ряд, согласно признаку Даламбера, сходится, так как:
 .
.
Тогда на основании признака Вейерштрасса функциональный
ряд (5.5) равномерно сходится для всех ![]() из
интервала
из
интервала ![]() .
.
Обозначим ![]() . Тогда
. Тогда ![]() - непрерывная на интервале
- непрерывная на интервале ![]() функция.
функция.
Покажем, что ![]() удовлетворяет
начальному условию
удовлетворяет
начальному условию ![]() и не выходит из области
и не выходит из области ![]() . В самом деле:
. В самом деле: ![]() .
Далее, переходя к пределу в неравенстве
.
Далее, переходя к пределу в неравенстве ![]() ,
получаем
,
получаем ![]() , т.е. не выходит за пределы области
, т.е. не выходит за пределы области ![]() .
.
III.
Докажем, что ![]() есть решение уравнения (5.3).
есть решение уравнения (5.3).
Так как ![]() равномерно на
равномерно на ![]() , то для любого
, то для любого ![]() найдётся
найдётся
![]() такой, что
такой, что
![]() ,
, ![]() для
для ![]() .
.
Поэтому, используя условие Липшица, имеем
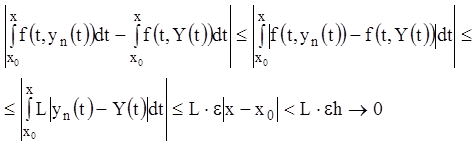
при ![]() , так
что
, так
что  при
при ![]() для
всех
для
всех ![]() ,
, ![]() .
.
Поэтому, переходя к пределу в соотношении (5.4),
определяющим ![]() , будем иметь:
, будем иметь:
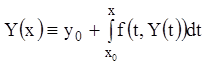 ,
, ![]() ,
,
т.е. ![]() является
решением интегрального уравнения (5.3), а, следовательно, и решением уравнения
(5.1), определённым и непрерывно дифференцируемом при
является
решением интегрального уравнения (5.3), а, следовательно, и решением уравнения
(5.1), определённым и непрерывно дифференцируемом при ![]() ,
и удовлетворяющим начальному условию
,
и удовлетворяющим начальному условию ![]() .
.
IV.
Докажем, что такое решение ![]() единственное. Пусть на
отрезке
единственное. Пусть на
отрезке ![]() кроме решения
кроме решения ![]() существует
другое решение
существует
другое решение ![]() , такое, что
, такое, что ![]() . Рассмотрим любой малый интервал
. Рассмотрим любой малый интервал ![]() ,
, ![]() , на
котором
, на
котором ![]() . Так как функции
. Так как функции ![]() и
и
![]() равны не во всех точках этого интервала,
то в некоторой точке
равны не во всех точках этого интервала,
то в некоторой точке ![]() , лежащей в интервале
, лежащей в интервале ![]() , абсолютная величина разности этих функций
, абсолютная величина разности этих функций
![]() достигает наибольшего значения
достигает наибольшего значения ![]() :
:
![]() .
.
Рассмотрим:

Или, если распространить
интегрирование на интервал ![]() ,
,
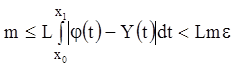 .
.
Тогда ![]() , что невозможно, так
как
, что невозможно, так
как ![]() можно выбирать сколь угодно малым.
можно выбирать сколь угодно малым.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.