Дифференциальные уравнения и математическое моделирование. Основные понятия дифференциальных уравнений. Метод Изоклин, страница 24

С целью упрощения изучения качественной картины поведения интегральных кривых уравнения (6.4) в окрестности особой точки (0,0) сделаем линейную подстановку (невырожденное линейное преобразование):

                                                    (6.6)

где  - некоторые постоянные, причем . Попытаемся подобрать коэффициенты преобразования (6.6) так, чтобы преобразованное уравнение (6.4) имело вид:

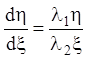,                                                          (6.7)

где и - некоторые постоянные числа.

Из (6.6) получаем , составляем производную 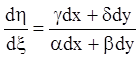. Разделим числитель и знаменатель правой части на  и заменим отношение  его значением из уравнения (6.4):

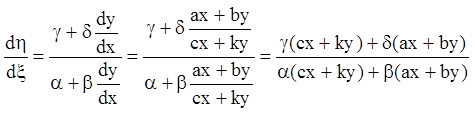.                        (6.8)

Правая часть равенства (6.8) должна иметь вид (6.7), поэтому должно выполняться тождество:

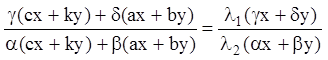.                                  (6.9)

Это тождество будет выполнено, если:

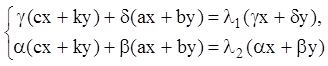.                                  (6.10)

Приравнивая коэффициенты при x и y , получаем две системы:

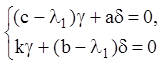                                                  (6.11)

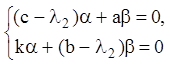                                                 (6.12)

Это линейные однородные системы, которые могут иметь ненулевые решения только при условии, что определитель системы равен нулю, т.е. что и  должны быть корнями уравнения

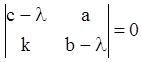,                                        (6.13)

которое можно записать в виде:

                                          (6.14)

Это уравнение называют характеристическим для уравнения (6.4), а его корни – характеристическими числами.

Предположим, что уравнение (6.14) имеет два различных корня . Подставляя один из них, напримерв (6.11), а другой в (6.12), получим (с точностью до множителя пропорциональности) и , а из второй -  и , причем условие  будет выполнено. Таким образом, уравнение (6.4) при помощи подстановки (6.6) привелось к виду (6.7). А уравнение (6.7) легко интегрируется разделением переменных:

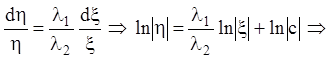
                                                   (6.15)

Исследуем решение (6.15) для различных случаев значений корней и  уравнения (6.14).

Корни и  действительны и одного знака.

Без ограничения общности предполагаем, что . Все интегральные кривые (6.15) проходят через начало координат (), касаются оси , т.к.

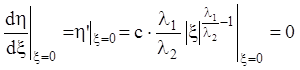                                        (6.16)

Из этого следует, что все интегральные кривые примыкают к особой точке с одним и тем же направлением, все они касаются оси  . Интегральные кривые  примыкают к особой точке тоже с определенным направлением (вдоль оси ), но отличным от направления интегральных кривых (6.15).Особая точка с таким расположением интегральных кривых называется узлом (рис.16).

Так как в окрестности особой точки исходного уравнения (6.4) мы будем иметь ту же качественную картину расположения интегральных кривых, то особая точка   уравнения (6.4) тоже будет узлом.

Корни  и действительны и разных знаков.

Тогда, 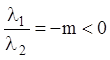. Интегральные кривые определяются уравнением

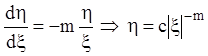                                                      (6.17)

В этом случае только два решения уравнения и  примыкают к особой точке. Все же остальные интегральные кривые, как показывает формула (6.17), не примыкают к особой точке, т.е.  не стремится к нулю при . При этом каждая из этих интегральных кривых обладает тем свойством, что при  точка , лежащая на ней, сначала приближается к особой точке (0,0), а затем начинает от нее удаляться. Особая точка такого типа называется седлом. В этом случае особая точка  уравнения (6.4) также является седлом.

Корни  и комплексные, но не мнимые:

.

Уравнение (6.7) в этом случае принимает вид:

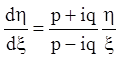                                                        (6.18)

Найдем  и из системы (6.12), где . Затем, считая и полагая в системе (6.11) , найдем, используя систему (6.12), что:

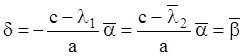                                                (6.19)

Поэтому преобразование (6.6) в этом случае запишется:

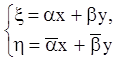                                                        (6.20)

Здесь  и  - комплексные, причем . Переменные  , неудобны, так как принимают при действительных x, y комплексные значения. Поэтому сделаем еще одну замену переменных:

,                                                      (6.21)