Таким образом, задача отыскания интегрирующего
множителя ![]() свелась к решению дифференциального
уравнения в частных производных (4.20), т. е. к задаче более сложной, чем
решение уравнения (4.1). Поэтому уравнение (4.20) будем решать в предположении,
что искомый интегрирующий множитель
свелась к решению дифференциального
уравнения в частных производных (4.20), т. е. к задаче более сложной, чем
решение уравнения (4.1). Поэтому уравнение (4.20) будем решать в предположении,
что искомый интегрирующий множитель ![]() является сложной
функцией вида
является сложной
функцией вида
![]() ,
(4.21)
,
(4.21)
где ![]() -
наперёд заданная функция
-
наперёд заданная функция ![]() .
.
Подставляя (4.21) в (4.20), получим линейное
однородное уравнение относительно ![]() . В самом деле
. В самом деле 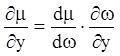 ;
; 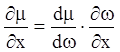 ,
тогда:
,
тогда:
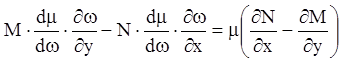 ;
;
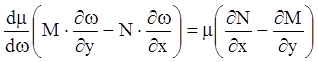 ;
;
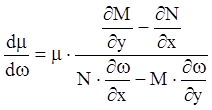 .
(4.22)
.
(4.22)
Из (4.22) делаем вывод, что предположение о существовании интегрирующего множителя в классе функций (4.21) справедливо лишь тогда, когда выполняется условие:
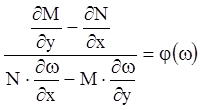 .
(4.23)
.
(4.23)
Тогда из уравнения (4.22) получаем:
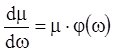 ,
(4.24)
,
(4.24)
решая которое, получаем:
 ;
;
![]() ;
;
![]() .
(4.25)
.
(4.25)
Отметим, что если функция ![]() неизвестная,
то условие (4.20) фактически даёт относительно неё уравнение в частных
производных:
неизвестная,
то условие (4.20) фактически даёт относительно неё уравнение в частных
производных:
 ,
,
т.
е. уравнение вида (4.20), где ![]() - произвольная функция
переменной
- произвольная функция
переменной ![]() . Методы решения таких уравнений будем
рассматривать позже.
. Методы решения таких уравнений будем
рассматривать позже.
![]() .
.
Р е ш е н и е. Здесь ![]() ,
, ![]() ,
,
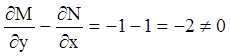 . Используем условие (4.23) и попробуем
подобрать функцию
. Используем условие (4.23) и попробуем
подобрать функцию ![]() , при которой (4.23) выполняется:
, при которой (4.23) выполняется:
 .
.
При
![]() условие (4.23) выполняется, причём
условие (4.23) выполняется, причём 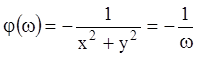 . Тогда, согласно с (4.25), получаем:
. Тогда, согласно с (4.25), получаем:
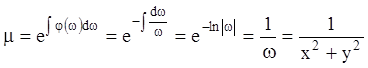 .
.
Умножив уравнение на этот множитель, получим уравнение в полных дифференциалах:
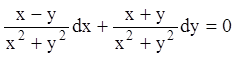 .
.
Для интегрирования уравнение удобно переписать в виде:
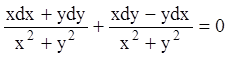 .
.
Откуда
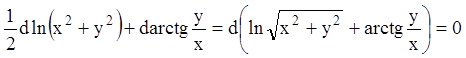 ,
,
и таким образом общий интеграл уравнения запишется:
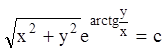 .
.
Задача нахождения ![]() значительно
упрощается в предположении, что
значительно
упрощается в предположении, что ![]() или
или ![]() .
.
1.
Если ![]() , то (4.20) запишется:
, то (4.20) запишется:
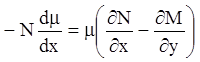 ;
;
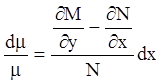 .
.
Если:
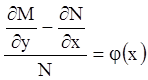 ,
(4.26)
,
(4.26)
то:
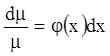 ;
;
![]() ;
;
![]() .
(4.27)
.
(4.27)
П р и м е р 3. Решить уравнение
![]() .
.
Р е ш е н и е. Здесь ![]() ,
, ![]() , откуда
, откуда 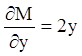 ,
, 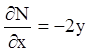 . Тогда (4.26) получаем:
. Тогда (4.26) получаем:
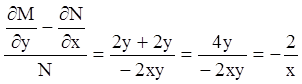 .
.
Тогда из (4.27):
 ;
;
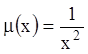 .
.
Умножая на интегрирующий множитель, получаем
 -
уравнение в полных дифференциалах.
-
уравнение в полных дифференциалах.
Его левую часть можно представить в
виде 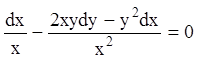 т. е.
т. е. 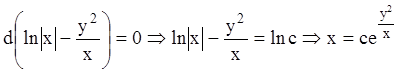 -
общий интеграл.
-
общий интеграл.
2. Аналогично, если ![]() , то
(4.20) запишется:
, то
(4.20) запишется:
 ;
;
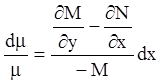 .
.
Если:
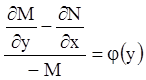 , (4.28)
, (4.28)
то:
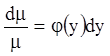 ;
;
![]() ;
;
![]() .
(4.29)
.
(4.29)
П р и м е р 4. Решить уравнение
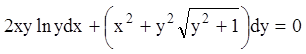 .
.
Р
е ш е н и е. Здесь ![]() ,
, ![]()
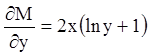 ,
, 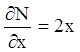 .
.
Из (4.28) получаем:
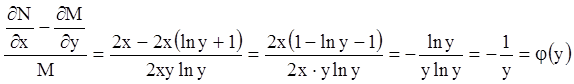 .
.
Тогда разделяющий множитель 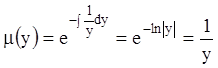 т. е.
т. е.
 .
.
Исходное уравнение является (после умножения на 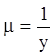 ) уравнением в полных дифференциалах:
) уравнением в полных дифференциалах:
 ;
;
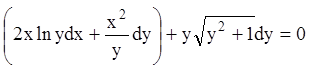 .
.
Его можно записать в виде:
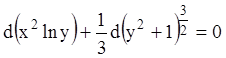 ;
;
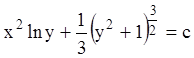 -
общий интеграл уравнения.
-
общий интеграл уравнения.
З а м е ч а н и е 2. Впервые Л. Эйлер указал на целый ряд типов дифференциальных уравнений 1-го порядка, которые интегрируются при помощи интегрирующего множителя. После Эйлера в исследованиях Абеля (1802-1829), Г. Якоби (1804-1851), О.М. Коркина (1837-1908) указано много типов дифференциальных уравнений 1-го порядка, интегрирование которых можно проводить при помощи интегрирующего множителя.
Из рассмотренных нами ранее типов уравнений 1-го порядка интегрируются методом интегрирующего множителя уравнения с разделяющимися переменными
![]() ,
,
там 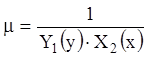 , и
его называют разделяющим множителем.
, и
его называют разделяющим множителем.
Для линейного уравнения ![]() ,
которое можно записать в виде
,
которое можно записать в виде ![]() , где
, где ![]() ,
, ![]() ,
, 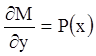 ,
, 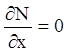 .
Интегрирующий множитель можно найти, положив, что
.
Интегрирующий множитель можно найти, положив, что ![]() , тогда
из (4.20) имеем:
, тогда
из (4.20) имеем:
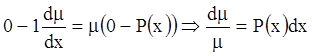 .
.
Интегрируя получаем:
![]() ;
;
![]() .
.
Это и есть рассмотренный нами выше метод Эйлера интегрирования линейного уравнения.
Отметим, что поскольку однородное уравнение вида
![]()
заменой ![]() приводится
к уравнению с разделяющимися переменными, то их тоже можно интегрировать с
помощью интегрирующего множителя. При этом:
приводится
к уравнению с разделяющимися переменными, то их тоже можно интегрировать с
помощью интегрирующего множителя. При этом:
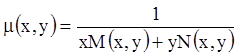 .
.
В самом деле, преобразуем исходное уравнение, если ![]() и
и ![]() однородные
функции измерения
однородные
функции измерения ![]() :
:
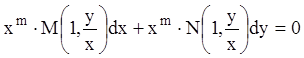 .
.
Сделаем
замену 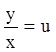 ,
, ![]() ,
, ![]() , тогда:
, тогда:
![]()
или:
![]() .
.
Это уравнение с разделяющимися переменными:
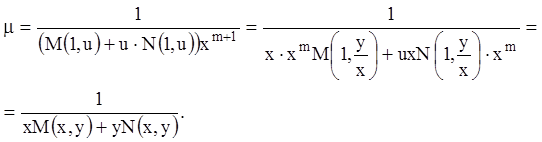
Тема: Теорема
существования и единственности решения уравнения ![]() .
Уравнения первого порядка не разрешенные относительно производной
.
Уравнения первого порядка не разрешенные относительно производной
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.