Дифференциальные уравнения и математическое моделирование. Основные понятия дифференциальных уравнений. Метод Изоклин, страница 16

ПЛАН

5.1     Теорема существования и единственности решения уравнения

5.2  Уравнения первого порядка не разрешенные относительно производной. Основные понятия

5.3 Типы дифференциальных уравнений, не разрешенных относительно производной

5.4   Теорема существования и единственности для уравнений, не разрешенных относительно производной

5.1 Теорема существования и единственности решения уравнения

Класс дифференциальных уравнений, которые интегрируются в квадратурах, очень ограничен, поэтому ещё со времён Эйлера приближённые методы решения дифференциальных уравнений в теории этих уравнений приобрели большое значение.

Сейчас в связи с наличием персональных быстродействующих компьютеров иногда бывает целесообразно применять приближенные методы даже в тех случаях, когда уравнение интегрируется в квадратурах. Однако для того, чтобы применять тот или иной метод приближённого интегрирования дифференциального уравнения, надо, прежде всего быть уверенным в существовании искомого решения, а так же и в его единственности, так как при отсутствии единственности возникает вопрос, какое именно решение требуется приближённо определить.

Приводимое нами доказательство теоремы существования и единственности решения уравнения  дано Пикаром в 1893 г. Это доказательство проводится так называемым методом последовательных приближений. По своей сути он является конструктивным и не только устанавливает существование и единственность решения, но и даёт способ построения приближённого решения с определённой степенью точности.

Т е о р е м а  1 (о существовании и единственности решения).

Если в уравнении:

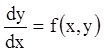                                                       (5.1)

функция  непрерывна по обоим переменным в прямоугольнике : , , где ,  - некоторые положительные постоянные числа и удовлетворяет в  условию Липшица по переменной :

,

где  - постоянная Липшица и ,  при , тогда существует единственное решение ,  уравнения (5.1), удовлетворяющее условию

,                                                    (5.2)

где 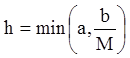,  в области .

Дадим некоторые пояснения условиям теоремы.

Нельзя утверждать, что искомое решение  уравнения (5.1), удовлетворяющее условию (5.2), будет существовать при , так как интегральная кривая  может выйти из прямоугольника  через его верхнюю или нижнюю стороны  (см. рис. 12) при некотором значении , , и тогда, если  и , решение уже не может быть определено (если  и , то решение тоже не может быть определено). Можно гарантировать, что интегральная кривая  не выйдет за пределы области  при  изменяющемся на отрезке , где  - наименьшее из двух чисел  и  (рис. 13), так как угловой коэффициент касательной к искомой интегральной кривой заключён между угловыми коэффициентами  и  прямых, изображенных на рис. 13. Если эти прямые, между которыми заключена искомая интегральная кривая, выходит за пределы прямоугольника  через его горизонтальные стороны , то абсциссы пересечения этих сторон будут 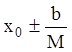, следовательно, абсцисса точки выхода интегральной кривой из прямоугольника  может быть лишь меньше, или равна 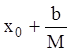 и больше, или равна .

Условие Липшица

,

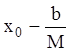может быть заменено более грубым, но легко проверяемым условием существования ограниченной по модулю частной производной  в области . Действительно, если в прямоугольнике  , то по теореме о конечном приращении получим:

,

где . Следовательно, точка , поэтому  и .

Нетрудно привести примеры функций  (например,  в окрестности точек ), для которых условие Липшица выполнено, но производная  в некоторых точках не существует, следовательно, условие  является более грубым, чем условие Липшица.

Д о к а з а т е л ь с т в о. Доказательство существования решения уравнения (5.1) сведём к доказательству существования решения эквивалентного интегрального уравнения. Действительно, если некоторая функция  является решением уравнения (5.1), то имеет место тождество 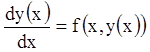. Интегрируя последнее равенство в пределах от  до , получаем:

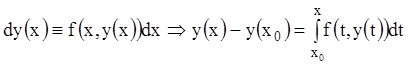.                                    (5.3)