Дифференциальные уравнения и математическое моделирование. Основные понятия дифференциальных уравнений. Метод Изоклин, страница 32

то есть получим уравнение первого порядка, в которое явным образом не входит аргумент x. Рассмотрим несколько возможных вариантов уравнения (7.27).

1)  Пусть (7.27) можно легко разрешить относительно , т.е.

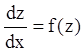,                            (7.28)   

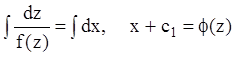 .                                    (7.29)

а)  если уравнение (7.29) можно разрешить относительно z, то из (7.29) следует  и, учитывая замену , получаем:

  и т.д.

б)  если (7.29) нельзя разрешить относительно z, то рассматривая z как параметр, получаем  ():

Т.к.: 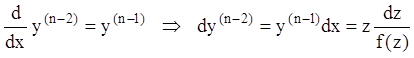 ,   из (7.28) следует  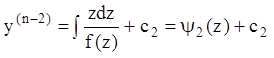 . Аналогично:

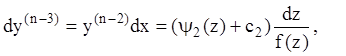
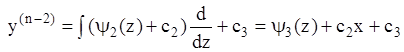 и т.д.

2)  Пусть (7.27) можно разрешить относительно z, т.е. 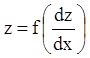, тогда, вводя параметр 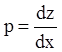, получаем:

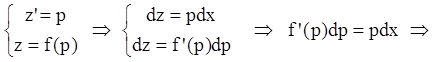
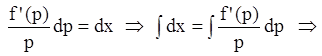
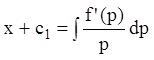.                                                 (7.30)

а) если из равенства (7.30)  можно найти р, то т.к.  . Т.к. , то:

  и т.д.

б)  если равенство (7.30) нельзя разрешить относительно р, тогда находим:

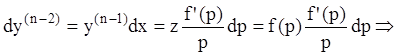
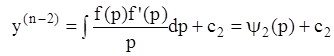  и т.д.

Окончательно получаем зависимость:

,

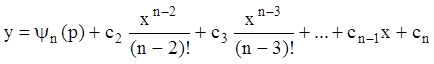которая вместе с 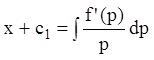 дает общее решение уравнения (7.26) в параметрической форме.

3)  Если уравнение (7.26) нельзя разрешить относительно того или другого аргументов, но имеется возможность его параметризировать, т.е. заменить:

.                                      (7.31)

Тогда:

.

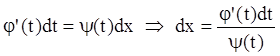Откуда:

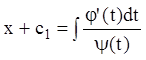.                                                  (7.32)

Далее, последовательно интегрируя, находим:

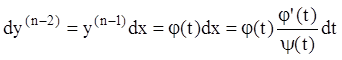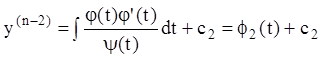 ,  и  т.д.

Снова получаем y, выраженный через параметр t, который вместе с (7.32) дает общее решение уравнения (7.26) в параметрической форме.

III.   Уравнение вида:

.                                       (7.33)

Замена  приводит (7.33) к уравнению второго порядка:

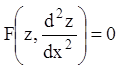.                                            (7.34)

1)  Положим, что уравнение (7.34) можно разрешить относительно :

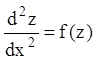.                                               (7.35)

Умножив обе части последнего равенства на 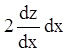, получим:

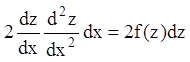 или ,

откуда:

.

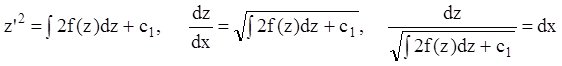Значит:

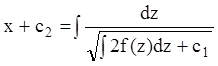.                                        (7.36)

После вычисления интеграла возможны следующие случаи:

а)  уравнение (7.36) можно разрешить относительно z, т.е.  . Или по определению производной 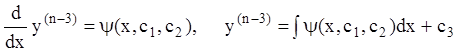 и  т.д.

б)  если  (7.36) нельзя разрешить относительно z, тогда:

.

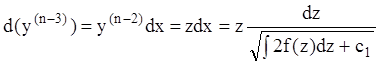Интегрируя, находим:

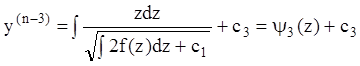 и  т.д.

Интеграл уравнения будет в параметрической форме.

2)  Если (7.34) нельзя разрешить относительно , но это уравнение имеет параметрическое изображение:

, тогда

,

.

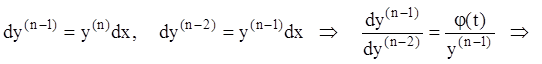
Тогда:

,

т.е. задача свелась к интегрированию уравнения вида (7.26)     (случай 3).

П р и м е р 4. Решить уравнение  .

Р е ш е н и е. Умножаем на :

.

,           

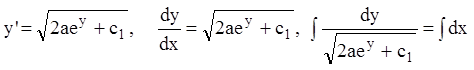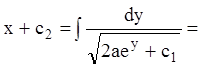
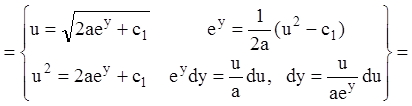
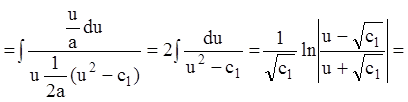
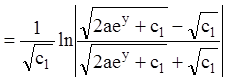, т.е. .

7.3 Понижение порядка дифференциального уравнения

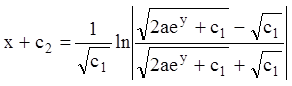Понизить порядок уравнения

                                            (7.37)

можно в случаях, если: 1) уравнение явно не содержит искомой функции y; 2) уравнение не содержит явно независимой переменной x;  3) уравнение однородное относительно искомой функции и ее производных;  4) уравнение однородное относительно переменных и их дифференциалов;  5) левая часть уравнения есть полная производная по x какого-то дифференциального выражения (n-1)-го порядка и т.д. Рассмотрим некоторые из этих случаев.

1)  Уравнение вида

,                                      (7.38)

которое не содержит . Положив в (7.38) , будем иметь

.                                           (7.39)

Порядок уравнения понизился на k единиц, и, если бы мы сумели найти общий интеграл уравнения (7.39), то имели бы:

                                           (7.40)

или:

,                            (7.41)

т.е. интегрируемый тип, рассмотренный в предыдущем параграфе. Зависимость (7.41) называют промежуточным интегралом уравнения (7.37).

П р и м е р. Решить уравнение  .

Р е ш е н и е. Это уравнение вида (7.38). Понижающая замена . Тогда уравнение запишем  . Это уравнение с разделяющимися переменными:

 

;

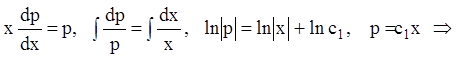
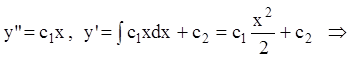
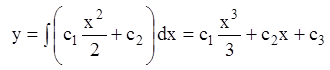- общее решение исходного уравнения,

где   - произвольные постоянные.

2)  Уравнение (7.37) не содержит явно x, т.е. уравнение вида:

.                                            (7.42)

Замена:

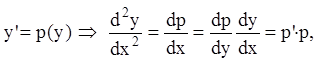
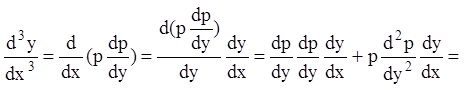
` и т.д.

Подставив эти выражения последовательных производных в (7.42), получим уравнение (n-1)-го порядка: