Дифференциальные уравнения и математическое моделирование. Основные понятия дифференциальных уравнений. Метод Изоклин, страница 13

Т е о р е м а  1. Если функции  и  в уравнении (4.1) в заданной области изменения ,  непрерывные и имеют непрерывные частные производные, то необходимым и достаточным условием того, что уравнение (4.1) является уравнением в полных дифференциалах , является тождество:

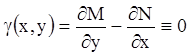,                                            (4.3)

а общий интеграл уравнения выражается равенством:

.                                                (4.4)

Н е о б х о д и м о с т ь. Если уравнение (4.1) является уравнением в полных дифференциалах, то выполняется равенство (4.3).

Д о к а з а т е л ь с т в о. Если уравнение (4.1) является уравнением в полных дифференциалах, то его левая часть удовлетворяет (4.2). Из (4.2) следует, что:

 и .                                   (4.5)

Так как по условию теоремы функции  и  имеют непрерывные частные производные, то смешанные производные функции  не зависят от порядка дифференцирования, т. е.:

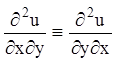.                                            (4.6)

Тогда из (4.5) следует: 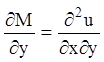 и 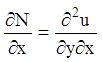. Так как правые части двух последних равенств равны (4.6), то левые части тоже равны, т. е. 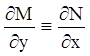 и функция 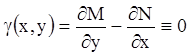 ч. т. п.

Д о с т а т о ч н о с т ь. Если для уравнения (4.1) выполняется условие (4.3), то уравнение (4.1) является уравнением в полных дифференциалах и его интеграл можно построить.

Д о к а з а т е л ь с т в о. Для построения функции  имеем равенство (4.5). Интегрируя равенство:

по переменной  ( считаем параметром), получаем:

,                   (4.7)

где  - произвольная постоянная переменной . Для её определения дифференцируем (4.7) по переменной  и используем второе равенство (4.5):

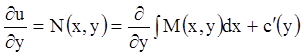
или

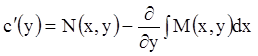.                                       (4.8)

Так как левая часть равенства (4.8) является функцией только от , то покажем, что правая часть (4.8) тоже не зависит от . В самом деле

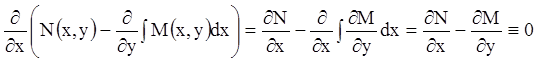
в силу тождества (4.3). Значит, правая часть (4.8) не зависит от переменной . Для обоснования равенства 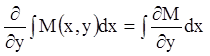 использовали условие непрерывности функции  и .

Тогда, интегрируя равенство (4.8), получаем:

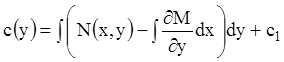,                                (4.9)

где  - произвольная постоянная. После подстановки (4.9) в (4.7) получили интеграл  и общий интеграл (4.4).

З а м е ч а н и е 1. Условие (4.3) впервые получил Л. Эйлер в 1739 г. и одновременно с ним К. Клеро.

П р и м е р 1. Найти общий интеграл уравнения

.

Р е ш е н и е. Здесь , . Условие (4.3) выполнено, так как 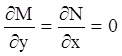 и , т. е. имеем уравнение в полных дифференциалах. Аналогично (4.7) находим

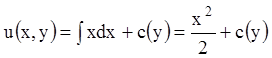.                                  (4.10)

Дифференцируя это равенство по , с учётом (4.5) получаем:

, .

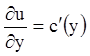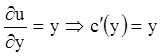Интегрируя последнее равенство по , находим:

.

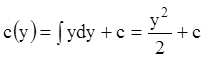Подставляя найденное значение  в (4.10), получаем:

.

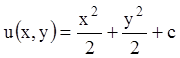Таким образом, получаем общий интеграл (4.4)

.

Другой метод интегрирования уравнений в полных дифференциалах основан на использовании криволинейных интегралов, которые не зависят от пути интегрирования.

Известно, что криволинейный интеграл вдоль простой дуги , которая лежит в области допустимых значений уравнения в полных дифференциалах

,

где  и  - концевые точки дуги , не зависит от выбора пути интегрирования.

Таким образом, интеграл уравнения (4.1) при условии (4.3) можно записать в виде

,                                    (4.11)

где  - произвольная кусочно-гладкая кривая, которая принадлежит О.Д.З. уравнения и соединяет произвольные точки  и  этой области.

В частности, ради простоты, за путь интегрирования  можно выбрать ломаную, части которой параллельны осям координат  и  (рис. 10).

В первом случае (рис. 10) из (4.11) получаем:

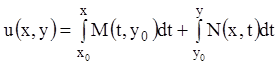.                               (4.12)

Во втором случае (рис. 11), получаем:

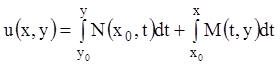.                                     (4.13)

П р и м е р 2. Решить уравнение:

.

Р е ш е н и е. Здесь , . Условие (4.3) выполнено, так как 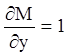; 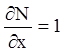. Значит, это уравнение в полных дифференциалах. Из (4.12) имеем:

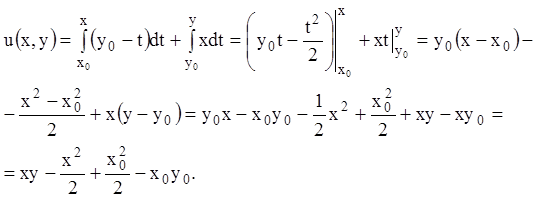
Из (4.13) получаем:

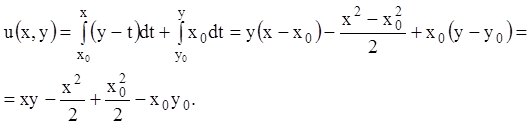
Так как ,  - постоянные величины, то можно положить

и, таким образом, искомый общий интеграл уравнения имеет вид

.

4.2 Метод интегрирующего множителя