Дифференциальные уравнения и математическое моделирование. Основные понятия дифференциальных уравнений. Метод Изоклин, страница 26

Р е ш е н и е. Учитывая, что в нашем случае

, составляем характеристическое уравнение (6.14)  . Получаем:

,

т.е. корни действительные и разные. Составляем , откуда следует, что особая точка (0,0) для рассматриваемого уравнения является седлом.

П р и м е р 2. Исследовать поведение интегральных кривых уравнения 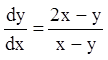 в окрестности точки (0,0).

Р е ш е н и е. В рассматриваемом случае  и характеристическое уравнение запишется:

.

Так как , то особая точка (0,0) для данного уравнения является центром.

П р и м е р 3. Исследовать поведение интегральных кривых уравнения 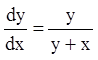  в окрестности точки (0,0).

Р е ш е н и е. В данном  уравнении и характеристическое уравнение имеет вид . Так как  и , но , то особая точка (0,0) является вырожденным узлом. Общее решение .

П р и м е р 4. Исследовать поведение интегральных кривых уравнения 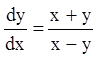  в окрестности точки (0,0).

Р е ш е н и е. В данном  уравнении и характеристическое уравнение имеет вид . Так как , то рассматриваемая особая точка является фокусом.

З а м е ч а н и е. Исследование интегральных кривых в окрестности изолированной особой точки впервые провел А. Пуанкаре и дал классификацию особых точек в 1881 г. в работе "О кривых, определяемых дифференциальными уравнениями". Результаты его исследований были потом продолжены и обобщены норвежским математиком Бендиксоном в 1901 г. Труды Пуанкаре (1854-1912 г.) положили начало качественной теории дифференциальных уравнений ( исследование поведения интегральных кривых во всей области определения правой части уравнения  без его интегрирования).

6.2 Особые решения дифференциальных уравнений первого порядка вида

Особым решением дифференциального уравнения первого порядка называется решение, которое во всех своих точках не обладает свойством единственности, т.е. его график сплошь состоит из особых точек.

Выше нами рассмотрены изолированные особые точки, которые получены из условия разрывности функции в точке . Теперь же предполагая, что  непрерывна в окрестности точки , рассмотрим точки, в которых нарушено второе условие теоремы существования и единственности решения – условие Липшица, или более грубое условие – ограниченность частной производной . Поэтому особые решения уравнения

                                                            (6.35)

могут проходить лишь через те точки, в окрестности которых становится неограниченной, т.е.

,                                                      (6.36)

при , где М – любое, как угодно большое положительное число. Условие (6.36) есть необходимое условие того, чтобы через точку проходило особое решение уравнения (6.35).

Отсюда получаем следующий алгоритм для нахождения особого решения уравнения (6.35) с непрерывной правой частью:

Находим геометрическое место точек области D, в которых выполняется условие (6.36).

Проверяем, будут ли полученные геометрические места точек решением уравнения (6.35).

Проверяем, нарушается ли свойство единственности в каждом из полученных таким образом решений.

Если все три условия выполняются, то найденное решение (а может быть и несколько решений) есть особое решение уравнения (6.35).

Для решения п.1 предложенного выше алгоритма в качестве искомого геометрического места рассматривают уравнение 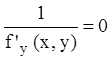, т.к. это уравнение определяет некоторую кривую, в точках которой может быть нарушена единственность.

П р и м е р 1. Найти особые решения уравнения  .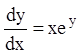

Р е ш е н и е. Здесь - непрерывная функция в любой замкнутой области  плоскости XOY, и ограничена в . Следовательно, данное уравнение особых решений не имеет.

П р и м е р 2. .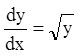

Р е ш е н и е. Здесь 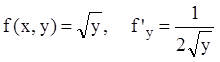. Функция 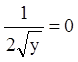 , т.е.  или  может быть особым решением. Очевидно, что это решение исходного уравнения. Интегрируя данное уравнение, получаем:

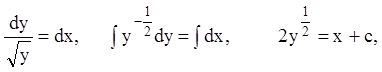
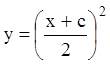() – общее решение.

Тогда через каждую точку линии проходит по крайней мере две интегральные кривые исходного уравнения: сама линия  и кривая семейства, составляющего общее решение . Отсюда, - особое решение уравнения.

П р и м е р 3. .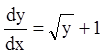

Р е ш е н и е. Здесь 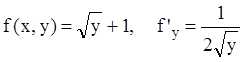 неограниченна при . Но не есть решение исходного уравнения (не выполняется проверка). А так как в остальных точках плоскости XOY выполняется условие теоремы существования, то уравнение особых решений не имеет.