Дифференциальные уравнения и математическое моделирование. Основные понятия дифференциальных уравнений. Метод Изоклин, страница 4

Итак, давление убывает с высотой по показательному закону в соответствии с барометрической формулой (1.8). Формула (1.8) на больших высотах (сравнимых по величине с радиусом Земли) дает большую погрешность. Это связано с тем, что пренебрегаем не только изменением температуры с высотой, но и изменением ускорения свободного падения ().

1.3.2 Уравнения в производных

Во многих случаях можно составить дифференциальные уравнения, в которых вместо дифференциалов содержатся производные, рассматриваемые как скорости изменения величин. В этом случаи мы вроде бы не рассматриваем приращения, но они учтены предварительно. Например, определяя скорость как 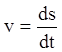, не пишем  и , хотя эти приращения фактически учтены, т. к. 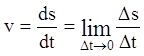. Аналогично ускорение в момент времени  выражается зависимостью:

.

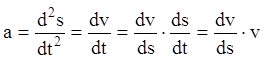П р и м е р 1. Материальная точка движется по прямой с постоянным ускорением . Начальная скорость точки , и к моменту  точка прошла расстояние . Найти закон движения точки.

Р е ш е н и е. По определению ,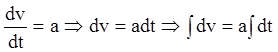

.                                                (1.9)

Находим  из начальных условий (при , )  и уравнение (1.9) запишется

.                                               (1.10)

Так как 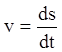, то 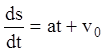 или , или , или

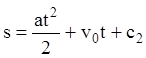.                                            (1.11)

Для нахождения  учитываем, что при  . Тогда после подстановки в (1.11) получаем . Следовательно уравнение движения запишется:

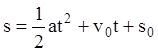          .                                          (1.12)

П р и м е р 2. Катер движется в спокойной воде со скоростью . На полном ходу его мотор выключается, и за 40 секунд скорость катера уменьшается до . Определить скорость катера через 2 минуты после остановки мотора.

Р е ш е н и е. На движущийся катер действует сила , где  - коэффициент пропорциональности. По закону Ньютона, 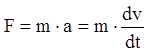. Следовательно, дифференциальное уравнение движения имеет вид:

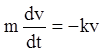.                                              (1.13)

Решаем его:

, ,

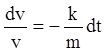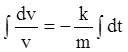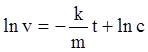
.                                                (1.14)

Учитывая начальные условия (,), получаем . Тогда общий закон движения имеет вид:

                                                (1.15)

Учитывая дополнительные условия (при 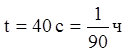 скорость ), из (1.15) получаем:

 или .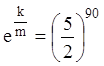

Тогда (1.15) запишется:

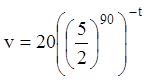.                                                  (1.16)

Получаем скорость катера через :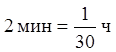

.

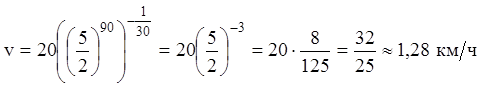О т в е т. Скорость катера через 2 минуты после остановки мотора станет равной .

1.3.3 Простейшие интегральные уравнения

Решение некоторых задач приводит к уравнениям, содержащим неизвестные функции под знаком интеграла. Такие уравнения называют интегральными. Они, в частности, возникают, когда при составлении уравнения используется геометрический смысл определённого интеграла как площади криволинейной трапеции и другие интегральные формулы (длина дуги, площадь поверхности, объем тела, работа силы и т. д.). В простейших случаях путём дифференцирования удается преобразовать интегральные уравнения в дифференциальные, которые интегрируются обычными методами.

П р и м е р 1. Найти кривую, проходящую через точку  и обладающую следующим свойством: если через любую точку кривой провести 2 прямые, параллельные координатным осям, до пересечения с последними, то полученный при этом прямоугольник делится кривой на 2 части, из которых одна (примыкающая к оси ) по площади вдвое больше другой.

Р е ш е н и е. Через любую точку  кривой проводим две прямые:  и . Согласно условию задачи, площадь  равна двум площадям . Т. к. 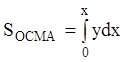, а площадь 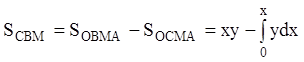, то получаем уравнение  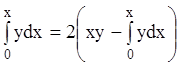или 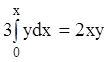. Продифференцируем по  обе части уравнения  или .

; ; ;

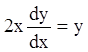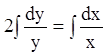или . Т. о., указанным свойством обладают параболы с вершинами в начале координат и с осями симметрии, совпадающими с осью . Используя начальное условие, находим , и поэтому искомой кривой является парабола .

1.4 Образование дифференциальных уравнений путём исключения произвольных постоянных из семейств кривых

Пусть дано уравнение семейства кривых, зависящие от одного параметра

.                                              (1.17)