Дифференциальные уравнения и математическое моделирование. Основные понятия дифференциальных уравнений. Метод Изоклин, страница 22

Это линейное дифференциальное уравнение первого порядка относительно x. Решим его, например, методом Бернулли.  Замена  . Подставляем в уравнение:

,   .

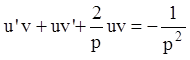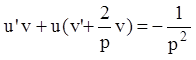v:     ;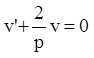

u:      ;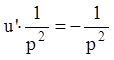

, ;

, ;

            ;

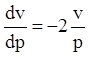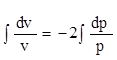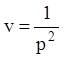
Тогда общее решение:     .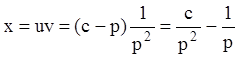

Подставляя найденное значение x в выражение для y, получим: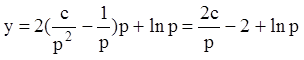.  Тогда общее решение в параметрическом виде примет вид:

.

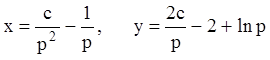У р а в н е н и е  К л е р о.

Уравнением Клеро называют уравнение вида:

                         (5.91)

(это вырожденное уравнение Лагранжа при ).  Такое название уравнение имеет потому, что впервые исследовал это уравнение в 1734 г. французский математик А. Клеро.

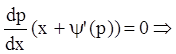
Решаем его так же, как и уравнение Лагранжа.  Замена  и    или  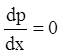   или  

 или                               (5.92)

Первое из равенств (5.92) дает . Следовательно, общее решение уравнения Клеро имеет вид:

,                        (5.93)

где с – произвольная постоянная.

Рассмотрим второе уравнение (5.92):

.

Предположим, что это уравнение разрешимо относительно p, для чего достаточно потребовать, чтобы функция  была непрерывной и не обращалась в 0. Тогда, разрешив его относительно p, получаем  . Следовательно:

.                          (5.94)

Покажем, что эта функция является решением уравнения Клеро. Действительно, из (5.94) с учетом второго уравнения (5.92) получаем:

, т.к.

т.е.                          (5.95)

Тогда, подставив в (5.91) значение (5.95),

 т.е.  ,

что и доказывает, что функция (5.94) является решением уравнения (5.91).

Покажем, что решение (5.94) не может быть получено из общего решения (5.93) ни при каком постоянном значении с. Из (5.93) следует, что общее решение есть семейство прямых, зависящих от параметра с. Допустим, что (5.94) входит в это семейство, тогда   есть линейная функция, т.е. . Продифференцировав данное тождество, получаем:

 или  .

Последнее равенство противоречит уравнению, определяющему (второе уравнение (5.92)).

Таким образом,  решение (5.94) или, что одно и то же, решени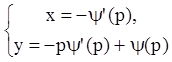е  не содержится в общем решении (5.93) и дальше покажем, что это особое решение.

П р и м е р 11. Решить уравнение.

.

Р е ш е н и е. Это уравнение Клеро вида (5.91). Замена . Тогда исходное уравнение запишется  .

                               

или

,

,

.

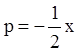Из исходного уравнения получаем: - общее решение – однопараметрическое семейство прямых. Исключая из уравнения и из уравнения 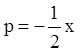 параметр p, получаем

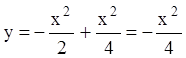 - особое решение.

5.4 Теорема существования и единственности для уравнений, не разрешенных относительно производной

Задача Коши для уравнения (5.7) ставилась так: найти такое решение уравнения (5.7), которое удовлетворяет заданным начальным условиям  . Геометрическая интерпретация этой задачи: среди всех интегральных кривых найти ту, которая проходит через точку . Выше мы показывали, что уравнение (5.7) чаще всего имеет несколько интегральных кривых, проходящих через точку . Если интегральные кривые, проходящие через точку , имеют в этой точке разные направления, то задача Коши имеет единственное решение. Если направления некоторых интегральных кривых в точке  совпадают, то задача Коши для уравнения (5.7) в этой точке имеет не единственное решение. Рассмотрим теорему, которая дает достаточные условия существования и единственности решения задачи Коши для уравнения (5.7).

Т е о р е м а. Пусть функция , стоящая в правой части уравнения (5.7), обладает следующими свойствами:

непрерывна вместе с частными производными первого порядка в некоторой замкнутой окрестности точки , где - один из действительных корней уравнения

                                                                (5.95)

.

Тогда существует в интервале , где h – достаточно мало, единственное решение уравнения (5.7), удовлетворяющее условию , для которого .

Д о к а з а т е л ь с т в о. Нетрудно видеть, что в данном случае относительно y' функция  удовлетворяет условиям теоремы существования неявной функции двух переменных. Поэтому уравнение (5.7) в некоторой замкнутой окрестности  точки   определяет y' как однозначную функцию

                                                            (5.96)