Уравнение первого порядка степени n вида
![]() (5.12)
(5.12)
где ![]() - непрерывные функции
в рассматриваемой области.
- непрерывные функции
в рассматриваемой области.
Предполагая, что в рассматриваемой области ![]() в силу основной теоремы алгебры
заключаем, что уравнение (5.12) определяет n значений
производной y'. Отбрасывая среди этих значений мнимые,
мы в некоторой окрестности точки (x0,y0) получаем m (m£n) дифференциальных уравнений первого порядка, разрешенных относительно
производной
в силу основной теоремы алгебры
заключаем, что уравнение (5.12) определяет n значений
производной y'. Отбрасывая среди этих значений мнимые,
мы в некоторой окрестности точки (x0,y0) получаем m (m£n) дифференциальных уравнений первого порядка, разрешенных относительно
производной
![]() . (5.13)
. (5.13)
Тогда каждое из уравнений (5.13) задает в некоторой
области D плоскости XOY свое
поле направлений. Следовательно, если ![]() в
области D удовлетворяет условиям теоремы существования
и единственности, то через каждую точку этой области проходит m
интегральных кривых. Проинтегрировав (5.13), получим общий интеграл уравнения
(5.7), т.е. совокупность общих решений
в
области D удовлетворяет условиям теоремы существования
и единственности, то через каждую точку этой области проходит m
интегральных кривых. Проинтегрировав (5.13), получим общий интеграл уравнения
(5.7), т.е. совокупность общих решений ![]() , или
общих интегралов
, или
общих интегралов ![]() . Рассмотренные ранее примеры
представляют уравнения рассмотренного вида.
. Рассмотренные ранее примеры
представляют уравнения рассмотренного вида.
П р и м е р 3. Решить уравнение:
![]()
Р е ш е н и е. Пусть ![]() , тогда
, тогда
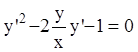 - квадратное уравнение
относительно y'. Отсюда,
- квадратное уравнение
относительно y'. Отсюда, 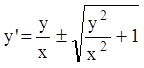 -
однородное дифференциальное уравнение первого порядка.
-
однородное дифференциальное уравнение первого порядка.
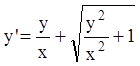 , или
, или 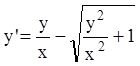 .
.
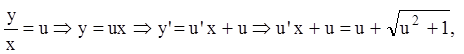
или ![]()
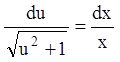 или
или 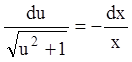 ,
,
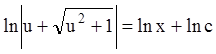 , или
, или 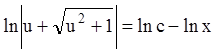
![]() или
или 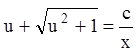 ,
, 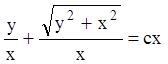 или
или 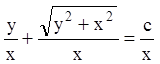
![]() , или
, или ![]()
![]() , или
, или ![]()
![]() , или
, или ![]()
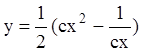 ,
, 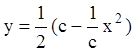 -
общий интеграл уравнения.
-
общий интеграл уравнения.
Уравнения вида
![]() , (5.14)
, (5.14)
в котором уравнение имеет некоторое (конечное или бесконечное) число вещественных корней:
![]() (5.15)
(5.15)
где ![]() .
.
Тогда из (5.15) находим ![]() , или
, или 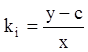 . Следовательно, уравнение (5.14) имеет
общий интеграл вида:
. Следовательно, уравнение (5.14) имеет
общий интеграл вида:
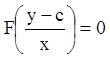 .
(5.70)
.
(5.70)
П р и м е р 4. Решить уравнение:
![]() .
.
Тогда, в силу (5.70) его общий интеграл:
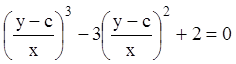 .
.
Уравнения вида
![]() ,
(5.71)
,
(5.71)
и такое, что его нельзя разрешить относительно y' (получили бы уравнение вида I), но можно разрешить относительно x, т.е.:
![]() ,
(5.72)
,
(5.72)
где ![]() - дифференцируемая
функция в некоторой области изменения y'. Сделаем
замену
- дифференцируемая
функция в некоторой области изменения y'. Сделаем
замену
![]() .
(5.73)
.
(5.73)
Тогда из (5.72)
![]() .
(5.74)
.
(5.74)
Используя замену (5.73), выразим y через p.
![]() .
.
Получаем: ![]() .
.
Таким образом, уравнение (5.71) имеет семейство решений:
![]() ,
(5.75)
,
(5.75)
которое называют общим решением в параметрической форме.
Если из системы (5.75) удается исключить параметр p, то
мы получаем общее решение ![]() , или общий интеграл
, или общий интеграл ![]() .
.
З а м е ч а н и е. Не всегда целесообразно в качестве
параметра выбирать y'. Иногда удобнее брать ![]() .
.
Рассмотрим теперь случай, когда уравнение (5.71) нельзя разрешить ни относительно y', ни x, но можно записать в параметрической форме:
![]() (5.76)
(5.76)
так, что для всех ![]() выполняется
тождество:
выполняется
тождество:
![]() (5.77)
(5.77)
Из (5.76) находим ![]() .
.
Тогда общее решение уравнения (5.71) представляется также параметрически:
![]() (5.78)
(5.78)
П р и м е р 5. Решить уравнение:
![]() .
.
Р е ш е н и е. Данное уравнение допускает разрешение
относительно x: ![]() .
Положив
.
Положив ![]() , имеем (из 5.75):
, имеем (из 5.75):
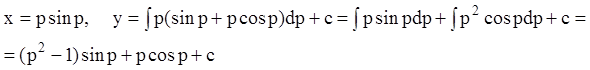
Таким образом, общий интеграл в параметрической форме:
![]() .
.
П р и м е р 6. Решить уравнение:
![]() .
.
Р е ш е н и е. Положим ![]() .
Тогда
.
Тогда ![]() .
.
Откуда, ![]() или
или 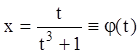 ,
,
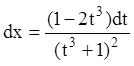 ,
, 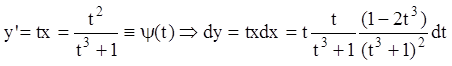 .
.
Таким образом, находим:
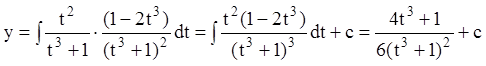 .
.
Значит, общее решение в параметрической форме:
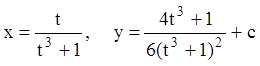 .
.
Уравнения вида
![]() . (5.79)
. (5.79)
Если уравнение разрешимо относительно y':
![]() , (5.80)
, (5.80)
где ![]() - один из
действительных корней уравнения (5.79). Полагая, что
- один из
действительных корней уравнения (5.79). Полагая, что ![]() находим
находим
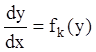 ,
, 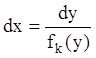 ,
, 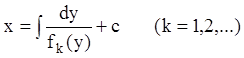 . (5.81)
. (5.81)
Легко видеть, что в этом случае решения уравнения (5.80)
будут также ![]() , где
, где ![]() - корни
уравнения
- корни
уравнения ![]() . Эти решения могут не содержаться в общем
интеграле (5.81) и могут оказаться особыми решениями уравнения (5.79).
. Эти решения могут не содержаться в общем
интеграле (5.81) и могут оказаться особыми решениями уравнения (5.79).
Если уравнение (5.79) разрешимо относительно y:
![]() ,
,
то, полагая ![]() и используя тождество
и используя тождество ![]() , получаем:
, получаем:
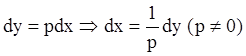 .
.
Т.к. ![]() , то
, то ![]() и
и 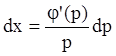 ,
,
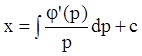 ,
, ![]() (5.82)
(5.82)
Таким образом, (5.82) является общим решением уравнения (5.79), записанным в параметрической форме.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.