Дифференциальные уравнения и математическое моделирование. Основные понятия дифференциальных уравнений. Метод Изоклин, страница 12

П р и м е р  3. Решить уравнение:

.                           (3.21)

Р е ш е н и е. Умножив обе части уравнения на множитель , получим:

.

Полагая , получаем  и , или . Интегрируя последнее уравнение по формуле (3.14) получаем общий интеграл:

,

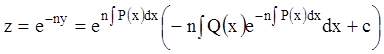или

.                (3.22)

П р и м е р  4. Решить уравнение:

.

Р е ш е н и е. 1-й способ:

;

;

:

; ;

; .

:

;

;

;

;

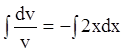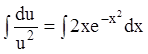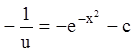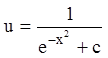 - общее решение.

2-й способ: делим на

.

Пусть , тогда

;

;

;

.

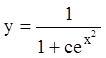3. Уравнение вида

                           (3.23)

переходом к обратной функции  можно свести к уравнению вида (3.16):

,

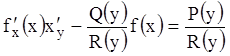а потом заменой  свести его к линейному относительно функции :

.

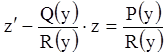Проинтегрировав его и сделав обратную замену получим общий интеграл уравнения (9).

П р и м е р  5. Решить уравнение:

.

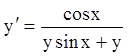Р е ш е н и е.

; .

Замена  и уравнение запишется

.

Интегрируя, получаем:

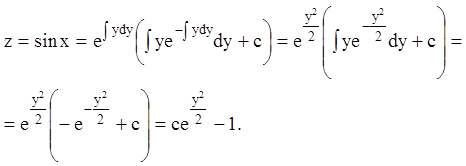
Или:

;

;

;

.

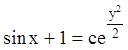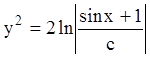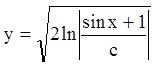4. В некоторых случаях к линейным можно свести уравнения при дополнительном условии, что известно одно или несколько его частных решений. К таким уравнениям принадлежит, например, уравнение Риккати:

,                   (3.24)

где , ,  - заданные непрерывные функции.

Действительно, пусть известно одно частное решение  уравнения (3.24), т. е.:

.

Введём замену:

,                        (3.25)

где . Подставив (3.25) в (3.24), получим:

или

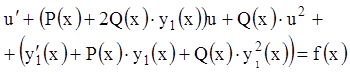
или

,                    (3.26)

где . Содержимое второй скобки равно , так как  является решением уравнения (3.24). Уравнение (3.26) является уравнением Бернулли при . Заменой  уравнение (3.26) сводится к решению линейного уравнения:

.

Интегрируя последнее уравнение, получаем:

.

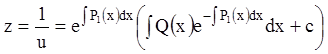Отсюда находим , а согласно (3.25) и решение уравнения Риккати:

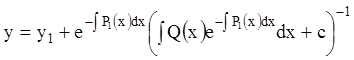,                    (3.27)

где .

В ы в о д. Если известно одно частное решение уравнение Риккати, то оно интегрируется при помощи двух квадратур.

П р и м е р  6. Проинтегрировать уравнение Риккати:

,

если известно частное решение .

Р е ш е н и е. Запишем уравнение в стандартном виде, разделив на :

.

Тогда замена  и уравнение запишется:

,

или преобразовав

,

или  - это уравнение с разделяющимися переменными:

;

;

;

.

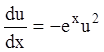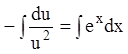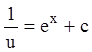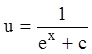Так как , то 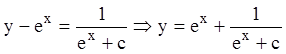 - общее решение.

5. Уравнение вида:

,      (3.28)

где ,  являются однородными функциями измерения , а  - однородная функция измерения . Это уравнение иногда называют уравнением Миндинга - Дарбу (если , то уравнение будет однородным 1-го порядка). Покажем, что уравнение Дарбу (3.28) приводится к уравнению Бернулли.

Так как функции ,  и  однородные, делаем замену , , , 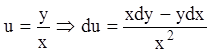причём,  будем считать независимой переменной. Получаем:

,

или, разделив на

;

.

Разделив на , получаем

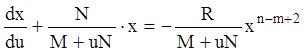.                (3.29)

Уравнение (3.29) является уравнением Бернулли (3.19) (при  - линейное уравнение) методы решения которого рассмотрены выше.

П р и м е р  7. Решить уравнение:

.

Р е ш е н и е. Это уравнение Дарбу, так как , . Замена , , тогда:

;

 или ,

разделив на , получим:

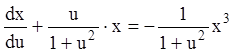 - уравнение Бернулли.

Интегрируя его, получаем:

.

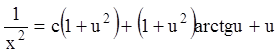Возвращаясь к переменной  (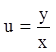), получим:

,

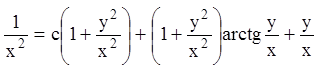или 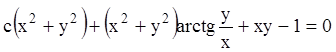 - общий интеграл уравнения Дарбу.

ЛЕКЦИЯ №4.

Тема: УРАВНЕНИЯ В ПОЛНЫХ ДИФФЕРЕНЦИАЛАХ. ИНТЕГРИРУЮЩИЙ МНОЖИТЕЛЬ И ЕГО НАХОЖДЕНИЕ.

ПЛАН

4.1 Интегрирование уравнений в полных дифференциалах

4.2 Метод интегрирующего множителя

4.1 Интегрирование уравнений в полных дифференциалах

Уравнение:

,                     (4.1)

левая часть которого является дифференциалом некоторой функции , называют уравнением в полных дифференциалах, т. е.

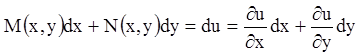.         (4.2)

Например,  является уравнением в полных дифференциалах, так как его можно представить в виде .

Таким образом, задача интегрирования уравнения в полных дифференциалах – это известная задача о восстановлении функции  по её полному дифференциалу. При интегрировании таких уравнений возникают два вопроса: как практически установить, что уравнение (4.1) является уравнением в полных дифференциалах? Как проинтегрировать это уравнение? Ответы даёт следующая теорема.