1) подробному разбору условий задачи и составлению чертежа;
2) составлению дифференциального уравнения рассматриваемого процесса;
3) интегрированию составленного дифференциального уравнения, определению общего его решения;
4) нахождению частного решения задачи на основании данных начальных условий;
5) нахождению вспомогательных параметров (при этом используются дополнительные условия задачи);
6) выводу общего закона рассматриваемого процесса и нахождению числовых значений искомых величин;
7) анализу ответа и проверке исходного положения задачи.
Некоторые из этих рекомендаций в зависимости от характера задачи можно не использовать.
При составлении дифференциальных уравнений 1-го порядка из условия геометрической или физической задачи обычно приходят к одному из следующих трёх видов уравнений:
1) дифференциальному уравнению в дифференциалах;
2) дифференциальному уравнению в производных;
3) простейшему интегральному уравнению с последующим преобразованием его в дифференциальное уравнение.
Рассмотрим, как составляются уравнения каждого из приведенных видов в отдельности.
При составлении дифференциальных уравнений 1-го
порядка часто бывает целесообразно применять так называемый метод
дифференциалов. Он заключается в том, что из условия задачи приближенным
путём составляются соотношения между дифференциалами (приращениями). При этом
делаются допущения, упрощающие задачу, и, вместе с тем, не отражающиеся на
результатах. Так, например, малые приращения величин заменяются их
дифференциалами; неравномерно протекающие физические процессы (неравномерное
движение точки, нагревание или охлаждение тела, истечение жидкости из сосуда и
т. д.) в течение малого промежутка времени ![]() рассматриваются
как равномерные, протекающие с постоянной скоростью. Эти допущения не
отражаются на правильности окончательных результатов вследствие того, что
замена приращений дифференциалами сводится к отбрасыванию бесконечно малых
высших порядков малости. Так как отношение дифференциалов функции и аргумента
является пределом отношения их приращений, то по мере того, как приращения
стремятся к нулю, наши допущения выполняются с большей точностью. Получающиеся
при этом дифференциальные уравнения оказываются точными, если они однородны
и линейны относительно дифференциалов.
рассматриваются
как равномерные, протекающие с постоянной скоростью. Эти допущения не
отражаются на правильности окончательных результатов вследствие того, что
замена приращений дифференциалами сводится к отбрасыванию бесконечно малых
высших порядков малости. Так как отношение дифференциалов функции и аргумента
является пределом отношения их приращений, то по мере того, как приращения
стремятся к нулю, наши допущения выполняются с большей точностью. Получающиеся
при этом дифференциальные уравнения оказываются точными, если они однородны
и линейны относительно дифференциалов.
Рассмотрим пример на составление дифференциальных уравнений с применением метода дифференциалов.
П р и м е р 1. Известно, что атмосферное давление с
высотой уменьшается. Найти зависимость давления ![]() от
высоты
от
высоты ![]() т. е.
т. е. ![]() .
.
Р е ш е н и е. Известно, что за величину атмосферного
давления принимается вес вертикального столба воздуха с площадью сечения ![]() . Проведём мысленно два горизонтальных
сечения этого столба на высотах
. Проведём мысленно два горизонтальных
сечения этого столба на высотах ![]() и
и ![]() . Разность давления на указанных высотах
. Разность давления на указанных высотах ![]() численно равна весу столбика воздуха между
двумя сечениями:
численно равна весу столбика воздуха между
двумя сечениями: ![]() , где
, где ![]() - масса
этого воздуха;
- масса
этого воздуха; ![]() - ускорение свободного падения.
Объем
- ускорение свободного падения.
Объем ![]() столбика равен
столбика равен ![]() ,
поэтому если средняя плотность воздуха в столбике равна
,
поэтому если средняя плотность воздуха в столбике равна ![]() ,
то
,
то ![]() , откуда
, откуда ![]() и
и
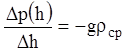 . (1.4)
. (1.4)
Обозначим плотность воздуха на высоте ![]() через
через ![]() . Тогда
при
. Тогда
при ![]() средняя плотность
средняя плотность ![]() .
Переходя к пределу в (1.4) при
.
Переходя к пределу в (1.4) при ![]() , получаем
дифференциальное уравнение
, получаем
дифференциальное уравнение
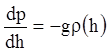 , (1.5)
, (1.5)
в котором функция ![]() также неизвестна.
также неизвестна.
Предположим, что температура воздуха одна и та же во всех слоях атмосферы. Тогда из закона Бойля - Мариотта или из уравнения газового состояния легко получить, что давление пропорционально плотности:
![]() (1.6)
(1.6)
Имеем ![]() , откуда
, откуда 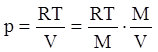 , где
, где 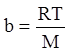 ;
; 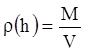 , где
, где ![]() -
универсальная газовая постоянная;
-
универсальная газовая постоянная; ![]() - полярная масса газа.
- полярная масса газа.
Из равенств (1.5), (1.6) получает дифференциальное уравнение
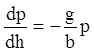 . (1.7)
. (1.7)
Умножив на ![]() и разделив на
и разделив на ![]() , получаем
, получаем
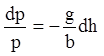 ,
, 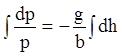 ,
, 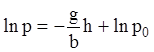
или
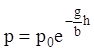 . (1.8)
. (1.8)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.