Дифференциальные уравнения и математическое моделирование. Основные понятия дифференциальных уравнений. Метод Изоклин, страница 18

Таким образом, полученное противоречие доказывает, что на интервале  . Таким же способом можно доказать, что на интервале  эти функции тоже совпадают.

Итак, решение, удовлетворяющее постоянному начальному условию, при наших предположениях существует, и единственно.

З а м е ч а н и е 1. Существование и единственность решения  доказаны лишь на отрезке , однако, взяв точку  за начальную, можно, повторив рассуждения, продолжить решение ещё на отрезок длины , если, конечно, в окрестности новой начальной точки выполнены условия теоремы существования и единственности решения. Продолжая этот процесс в некоторых случаях, можно продолжить решение на всю полуось  и даже на всю ось , если продолжить решение и в сторону меньших значений . Однако, возможны и другие случаи, даже если функция  определена для любых значений  и . Интегральная кривая становится непродолжаемой в случае приближения к точке, в которой нарушены условия теоремы существования и единственности решения, или интегральная кривая приближается к асимптоте, параллельной оси . Указанные случаи иллюстрируются следующими примерами:

П р и м е р 1. 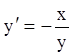, . Разделяя переменные и интегрируя, получаем , . Решение не продолжаемо за пределы интервала . В граничных точках  и  правая часть уравнения 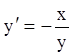 разрывна. Условия теоремы существования решения нарушены.

П р и м е р 2. , . Разделяя переменные и интегрируя, получаем 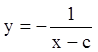, , , 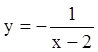и интегральная кривая продолжается лишь до асимптоты  (). Решением является лишь верхняя ветвь гиперболы.

З а м е ч а н и е 2. Отметим, что теорему существования единственности можно доказать и другими методами (например, используя принцип сжатых отображений (неподвижных точек), метод ломаных Эйлера) и при других предположениях относительно функции , например, теорема Осгуда [8], метод степенных рядов. В частности, условия существования решения задачи Коши решает теорема Пеано:

Пусть функция  непрерывна в прямоугольнике , причём, , 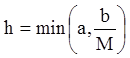. Тогда задача Коши на промежутке  имеет, по крайней мере одно решение .

Первое доказательство существования и единственности решения дифференциальных уравнений при определённых условиях принадлежит Коши (1789-1857). Рассмотрим некоторые примеры.

П р и м е р  3. Найти область существования решений уравнения .

Р е ш е н и е. Правая часть уравнения  непрерывна во всех точках плоскости xOy. В силу теоремы Пеано существования решения через каждую точку плоскости xOy проходит хотя бы одна интегральная кривая.

П р и м е р  4. Найти область единственности решения уравнения .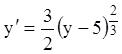

Р е ш е н и е. Правая часть уравнения 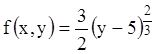 определена и непрерывна во всех точках плоскости xOy. Частная производная 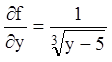 обращается в бесконечность при , т.е. на прямой, параллельной оси Ox. Следовательно, на прямой  возможно нарушение единственности. Легко видеть, что функция 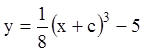 является решением данного уравнения, и каждая интегральная кривая проходит через точку, лежащую на прямой . Кроме того, уравнение имеет очевидное решение . Итак, через каждую точку прямой  по крайней мере проходят две интегральные кривые, и следовательно, в точках прямой  нарушается единственность. Во всех остальных точках плоскости уравнение имеет единственное решение.

П р и м е р 5. Найти второе приближение к решению уравнения

, если .

Р е ш е н и е. Запишем уравнение в виде 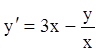, полагая . В качестве нулевого приближения будет . Используя формулу (5.4), строим первое приближение:

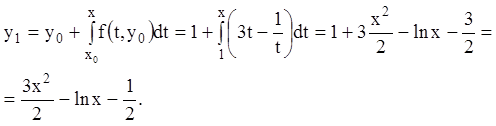
Строим второе приближение:

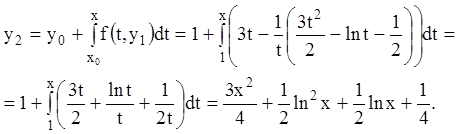
Найдём точное решение данного уравнения. Для этого представим его в виде 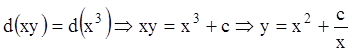. Используя начальное условие, получаем  - точное частное решение.

О т в е т: ,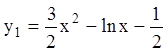

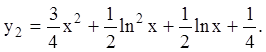
5.2 Уравнения первого порядка не разрешенные относительно производной. Основные понятия

Дифференциальное уравнение первого порядка, не разрешенное относительно производной, имеет вид:

,                                                      (5.7)

где F – заданная непрерывная функция 3-х переменных. Все введенные ранее понятия и определения для дифференциальных уравнений, разрешенных относительно производной, имеют место и для уравнений вида (5.7). Например, решением дифференциального уравнения (5.7) на некотором интервале (a,b) будем называть всякую функцию , определенную и непрерывно дифференцируемую на этом интервале, обращающую уравнение (5.7) в тождество  ,  .