Системы автоматического управления (САУ), конспект лекций, страница 25

(5) эквивалентно (7)

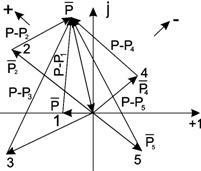
Рис. 51

p = j w. Поставим условие –  и посмотрим, что будет происходить а разностными величинами. Каждый разностный вектор будет разворачиваться на угол .

Пусть есть n корней характеристического уравнения l , из которых лежат в правой полуплоскости. Тогда в левой n–l. Определим приращение аргумента вектора комплексный ХУ при изменении – .

                                                                                         (8)

Характеристика принципа аргумента:

Превращение аргумента вектора корней характеристического уравнения при изменении частоты –  равна .

Для устойчивой работы должно быть l = 0

                                                           ;                                       (9)

Для того, чтобы система была устойчивой, необходимо чтобы приращение аргумента вектора комплексного ХУ при частоте от  равнялось .

В силу четности корней, (9) можно трансформировать следующим образом.

При ращение аргумента вектора комплексного характеристического уравнения (КХУ) при изменении частоты от 0 до  должна равняться .

                                                             ;                                         (10)

II формулировка (рабочая)

Для того, чтобы система n-ого порядка была устойчива, необходимо и достаточно чтобы годограф Михайлова начинался на действительной полуоси КП о проходил последовательно n квадратов этой плоскости в положительном направлении.