Рис. 49
Для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы все действительные корни и действительные части комплексных корней были отрицательными.
Наличие, хотя бы одной пары мнимых корней приводит САУ на границу устойчивости.
Интерпретация на комплексной плоскости.
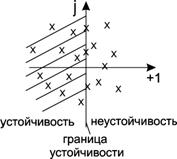
Рис. 50
Для решения задачи о устойчивости или неустойчивости САУ без непосредственного вычисления корней характеристического уравнения служит критерий устойчивости (КУ).
КУ подразделяются на алгебраические и частотные (АКУ) (ЧКУ).
АКУ позволяют по коэффициенту характеристического уравнения (с помощью определенных процедур) сделать заключение об устойчивости системы. Они просты, но они не позволяют оценить степень устойчивости САУ и по устойчивости в разомкнутой системы нельзя судить о том, будет система устойчивой в замкнутом состоянии или нет ЧКУ позволяют это сделать, но они более трудоемки и громоздки.
8.2 Критерий устойчивости Гурвица
Это алгебраический критерий устойчивости
![]() (5)
(5)
Для того, чтобы САУ была устойчивой, необходимо, чтобы все коэффициенты характеристического уравнения (ХУ) были больше 0 и достаточно, чтобы все диагональные миноры составленные из определителя Гурвица были больше нуля.
Определитель Гурвица – это квадратная матрица ранга n, составленная их коэффициентов характеристического уравнения.

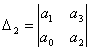
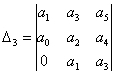
8.3. Критерий устойчивости Михайлова
Принцип аргумента.
![]()
Корни характеристического уравнения
![]() – векторы на КП.
– векторы на КП.
![]() (7)
(7)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.