Мультимедійний курс лекцій з опору матеріалів, страница 7

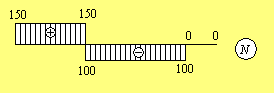
Зверніть увагу, що стрибки на епюрі N розташовуються в точках прикладення зовнішніх зосереджених сил і рівні величинам цих сил. Відповідно стрибок на лівому кінці епюри дає величину опорної реакції.

NII-II

4. Відкинемо ліву частину, замінимо її дію поздовжньої силою NI-I і складемо рівняння рівноваги в проекції на вісь z:

10

Лекція 2 (продовження – 2.4)

• Центральний розтяг-стиск. У багатьох елементах конструкцій виникають тільки поздовжні зусилля, що викликають у них деформації розтягу або стиску (стійки, елементи ферм, тяги, троси і т.п.). При цьому в місцях прикладення умовно зосереджених сил характер розподілу деформацій досить складний і відрізняється від розподілу деформацій на деякій відстані від цієї локальної області. Розмір цієї області дорівнює приблизно найбільшому з розмірів поперечного перерізу.
• Принцип Сен-Венана - Якщо сукупність деяких сил, прикладених до невеликої частини поверхні тіла, замінити статично еквівалентною системою інших сил, то така заміна не викличе суттєвих змін в умовах навантаження частин тіла, досить віддалених від місць прикладання вихідної системи сил.
• Як показує досвід, за межами цієї області деформації практично постійні і поперечні перерізи переміщуються паралельно своїм початковим положенням. На підставі цього вводиться гіпотеза плоских перерізів (Я. Бернуллі):
• Поперечні перерізи стержня, плоскі і перпендикулярні до осі стержня до деформації, залишаються плоскими і перпендикулярними після деформації.

• Напруження і деформації - Як було раніше сказано, задача визначення напружень завжди є статично невизначеною.
• Такі завдання вирішуються послідовним розглядом статичної, геометричної і фізичної сторін.
• В даному випадку маємо статичне рівняння, що зв'язує внутрішнє зусилля - поздовжню силу з напруженням:

Для обчислення інтеграла необхідно знати закон зміни напружень по перерізу. Цей закон можна встановити вивченням безпосередньо досліджуваних переміщень (деформацій). Оскільки приймається гіпотеза плоских перерізів, то при відсутності зовнішнього розподіленого поздовжнього навантаження, деформації постійні по перерізу і по довжині стержня (геометрія). З введеного раніше визначення деформацій у точці:

де l – абсолютна поздовжня деформація (видовження), l - довжина (базова довжина) стержня.

Дослідним шляхом встановлений фундаментальний (фізичний) зв'язок зусиль і видовжень (Р. Гук) і в наступному, напруження і деформацій (Коші, Навьє) у вигляді:

де Е – модуль пружності (фізична постійна матеріалу, що визначається експериментально).

Підстановка останнього співвідношення - закону Гука в інтегральне вираження з урахуванням сталості деформацій та напружень дає :

Нормальні напруження в поперечному перерізі прямо пропорційно величині поздовжнього зусилля і обернено пропорційно площі перерізу.

Абсолютну деформацію (видовження) стержня також можна визначити через поздовжнє зусилля (отримана таким чином залежність називається законом Гука в розгорнутому вигляді):

Формула для абсолютного видовження справедлива лише при постійній по довжині стержня поздовжній силі і незмінній площі поперечного перерізу! У разі змінної поздовжньої сили, наприклад, при врахуванні власної ваги вертикальних стержнів, та / або змінної площі необхідно використовувати інтегральний вираз:

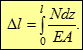
11

Лекція 2 (продовження – 2.5)

• Коефіцієнт Пуассона - при розтягу стержня поряд з поздовжньою деформацією (видовженням), яке визначається законом Гука, виникає поперечна деформація (звуження поперечного перерізу), що виражається в зменшенні поперечних розмірів стержня. Відносні поперечні деформації обчислюються як де b, a - розміри поперечного перерізу.

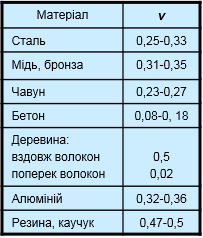
Експериментально встановлено, що існує лінійний зв'язок між поздовжньої і поперечної деформацією: де ν – коефіцієнт пропорційності, що називається коефіцієнтом Пуассона. Коефіцієнт Пуассона для певного матеріалу в межах пружних деформацій має постійне значення і знаходиться в межах від 0 до 0,5.