Мультимедійний курс лекцій з опору матеріалів, страница 15

Визначення координат центру ваги. Методи визначення положення центра ваги плоских фігур розглядалися в курсі теоретичної механіки, наприклад, метод розбиття на декілька елементарних елементів:

xC

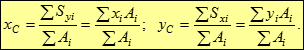
Тут xi, yi - координати центрів ваги простих фігур, для яких вони відомі або легко знаходяться. Нагадаємо процедуру визначення положення центра ваги: 1. вибрати довільну (початкову) систему координат x, y. 2. розбити задану фігуру на більш прості фігури. 3. обчислити статичні моменти і використовувати формули координат центру ваги.

Осі, що проходять через центр ваги фігури, називаються центральними. Можна показати, що відносно центральних осей, статичні моменти площі перетворюються в нуль.

Приклад 1 - Визначити положення центру ваги куткового поперечного перерізу.

1. Вибираємо систему координат x, y з початком в нижньому лівому куті перерізу.

2. Розбиваємо фігуру на два прямокутники, обчислюємо площі і координати центрів ваги кожного:

1

2

C

3. Обчислюємо статичні моменти і координати центру ваги всього перерізу:

O

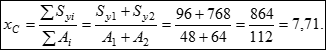
24

Лекція 7 (продовження – 7.2)

y

dy

• Моменти інерції площі поперечного перерізу:

- відцентровий момент інерції площі.

• осьові моменти інерції площі,

y



• полярний момент інерції площі.

x

dx

x

O

Моменти інерції площі використовуються при визначенні напружень при згині і крученні. Можна показати, що відцентровий момент інерції щодо осей, одна з яких збігається з віссю симетрії, дорівнює нулю. Справді, в цьому випадку елементарній площі dA з координатами (x, y) завжди буде відповідати така ж площа з координатами (-x, y) або (x, -y). Підсумовування (інтегрування) похідних xydA дасть нуль. Далі буде показано, що для будь-якої, в тому числі несиметричної, фігури можна знайти таке положення осей, при якому відцентровий момент перетворюється в нуль.

Полярний момент інерції не залежить від орієнтації координатних осей х, у та завжди дорівнює сумі осьових моментів інерції:

• Моменти інерції площі найпростіших перерізів:
• Прямокутник

• Трикутник

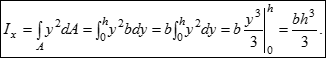
Елементарна площа має змінну ширину і залежить від її координати по осі y:

Відомо, що центр ваги прямокутника знаходиться на перетині осей симетрії (xC = b / 2, yC = h / 2). Для обчислення моментів інерції відносно центральних осей достатньо вважати, що координата y вимірюється від центральної осі xc і змінити межі інтегрування:

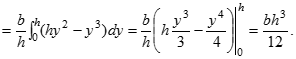
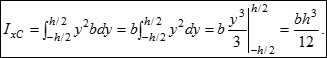
Момент інерції відносно центральної осі xC:

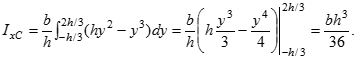
Аналогічно одержимо для інших осей:

Відцентровий момент інерції (по симетрії):

Момент інерції щодо центральної осі yC:

Полярний момент інерції:

25

Лекція 7 (продовження – 7.3)

• Круглий переріз:

Обчислимо спочатку полярний момент інерції:

• Моменти інерції площі складених перерізів
• обчислюються, так само як і при обчисленні координат центру
• ваги, методом розбиття на прості фігури, для яких
• відомі або легко обчислюються координати центрів ваги
• і моменти інерції.
• Наприклад, момент інерції кільцевого перерізу може бути
• обчислений як різниця моментів інерції круглого суцільного
• перерізу радіусу R і такого ж перерізу, але радіуса r.
• Зауважимо, що при додаванні моментів інерції по кожній
• з координатних осей для кожної з фігур моменти інерції
• повинні обчислюватися відносно осей, які є загальними
• для розглянутого перерізу і всіх складових фігур.
• Звідси випливає необхідність оперувати формулами,
• що дозволяють переходити від одних до інших осей.

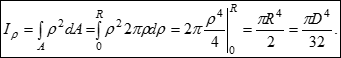
y

d

R

Моменти інерції щодо центральних осей з урахуванням симетрії:



x

У техніці часто використовують наближені значення (похибка менше 2%):

• Кільцевий переріз:

Достатньо змінити межі інтегрування:

• Залежність між моментами інерції
• при паралельному переносі осей

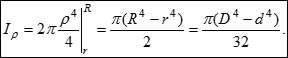
Моменти інерції щодо центральних осей з урахуванням симетрії:

Для тонкостінного кільця (t < 0,075R) можна наближено вважати, що  = Rср = const по його товщині A = 2Rсрt:

Аналогічно для осі y1:

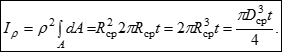
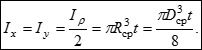
Формули спрощуються, якщо вихідні осі є центральними, т.я. SxC = SyC = 0:

У техніці іноді використовують наближені значення у вигляді: