Мультимедійний курс лекцій з опору матеріалів, страница 38

F

Оскільки вирішувати вручну 5 рівнянь теж досить складно можна залишити первісну систему з 8 рівнянь і вирішити її чисельно, наприклад, у системі MathCAD, в якій не потрібні будь-які підстановки і перетворення (продивитись).

Якщо напрями одного або двох стержнів відмінні від вертикального, то ця задача стає статично визначеною (для плоскої довільної системи сил можна скласти 3 незалежних рівнянь рівноваги) і невідповідність одного або двох розмірів проектним не викликатимуть початкових (монтажних) зусиль (балка лише змінить свій стан при збірці).

Видовження похилих стержнів визначаються відрізками, відрізаються перпендикулярами, опущеними з нового положення вузла (кінця стержня) на старий напрям стержня.

Приклад 5. Нехай до такої системи доданий ще один "зайвий" стрижень).

Система стає статично невизначеною, для якої можна скласти 3 рівняння рівноваги і 4 рівняння сумісності деформацій (разом з 4 співвідношеннями пружності виходить система 11 рівнянь):

l2м

B

б

l1м

l3м

lс

φ

B1

бx

74

Тепер у співвідношеннях пружності довжини 2-го і 3-го мідних стрижнів:

Лекція 18 (продовження – 18.5)

• Статично невизначені задачі при крученні - вирішуються так само, як і при інших видах деформацій, тобто послідовно розкриваються три сторони задачі (статика, геометрія і фізика). Специфіка полягає лише в тому, що складаються інші рівняння рівноваги, порівнюються кутові переміщення (кути закручування) і використовується фізичні співвідношення пружності, що зв'язує деформації і зусилля при крученні.
• Приклад. Вал круглого перерізу має ступеневу зміна діаметра (d = 0.707D) і навантажений трьома крутними моментами M.

1. Статика - відкидаємо жорсткі закріплення, замінюємо їх реактивними моментами :

MB

Складаємо моментне рівняння рівноваги відносно осі вала:

z

MA

Або:

B

Це рівняння єдине, що пов'язує навантаження і реактивні моменти. Всі інші (сума проекцій на координатні осі і суми моментів щодо осей x, y) звертаються в тотожності. Отже, задача є статично невизначеної з одним "зайвим" невідомим.

A

M

M

M

a

a

a

a

2. Геометрія - При наявності на обох кінцях вала нерухомих закріплень, сума кутів закручування на кожній з ділянок при будь-якому навантаженні повинна бути рівною нулю - Рівняння сумісності деформацій):

Побудуємо епюру крутних моментів:

0,9M

Рівняння сумісності приймає вид :

0,9M

Mz

+

3. Фізика – на кожній з ділянок кут закручування пов’язаний з крутним моментом в перерізі (співвідношення пружності):

Тут перші три доданки є кути закручування, обчислені для перерізу B, від дії трьох заданих моментів окремо. Останній доданок - кут закручування від дії невідомого опорного моменту MB.

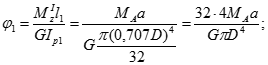
0,1M

0,1M

1,1M

1,1M

Співвідношення пружності:

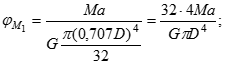
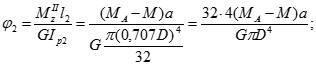
Отримані 6 рівнянь утворюють повну систему рівнянь із шістьма невідомими (2 реактивних моменти та 4 кута закручування). Підставимо співвідношення пружності у рівняння сумісності. Однакові співмножники винесемо за дужки та скоротимо:

2,1M

Побудуємо епюру кутів закручування:

2,1M

Підстановка цих співвідношень після деяких скорочень дає: звідки отримуємо:

φ2= -0,1Ma/(GIp1)

φ1=0,9Ma/(GIp1)

φ3= -0,275Ma/(GIp1)

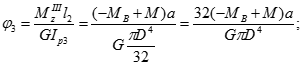
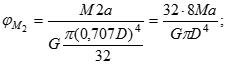
φ3= -0,525Ma/(GIp1)

+

Далі знаходиться з рівняння рівноваги лівий опорний момент і будується епюра крутних моментів звичайним чином або її можна побудувати без знаходження лівого опорного моменту, рухаючись справа.



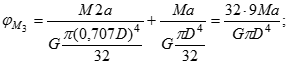
0

0

+

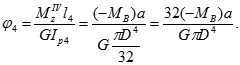
φ1 +φ2 +φ3 = 0,525Ma/(GIp1)

φ1 +φ2 = 0,8Ma/(GIp1)

Або:

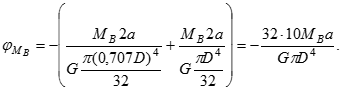
Виразимо, наприклад МА із рівняння рівноваги через МВ та підставимо в отримане рівняння:

Цю задачу можна вирішити інакше, використовуючи у якості основної системи статично визначену систему, для якої можна знайти кути закручування із використанням принципу незалежності дії сил від заданих моментів та невідомого опорного моменту:

Для побудови епюри кутів закручування доведеться обчислити для кожної з ділянок відносні кути, як це було показано при попередньому підході до вирішення.

75