Мультимедійний курс лекцій з опору матеріалів, страница 19

Оскільки тангенс має однакові значення для кутів, що відрізняються один від одного на 1800, отриманий вираз визначає дві площадки, що відрізняються один від одного на 900. Таким чином, обидві головні площадки взаємно перпендикулярні.

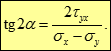
Зауважимо, що похідна нормальних напружень на похилій площадці по куту нахилу площадки рівна подвоєній величині дотичних напружень на цій площадці. Таким чином, на головних площадках дотичні напруження дорівнюють нулю.

Для визначення величини максимальних і мінімальних нормальних напружень необхідно знайти значення кута через arctg(…) і підставити у вихідний вираз для нормальних напружень. Але простіше безпосередньо використати наступні тригонометричні формули:

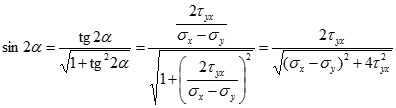
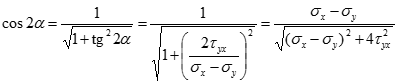
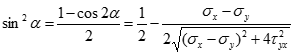
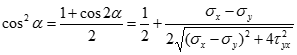
Підстановка цих тригонометричних функцій у формулу нормальних напружень дає для однієї із головних площадок:

Оскільки кут для другої головної площадки відрізняється від першої на 900, то синус і косинус подвійного кута змінює знак на протилежний, що приводить до зміни знаку другого доданку:

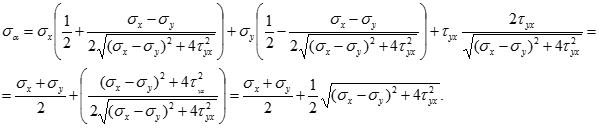
Таким чином, по двом головним площадкам діють головні напруження:

34

Лекція 10 (продовження – 10.3)

• Максимальні дотичні напруження. Існують площадки, на яких дотичні напруження досягають максимальних значень. Для визначення їх положення достатньо прирівняти до нуля першу похідну дотичних напружень по куту нахилу площадок:

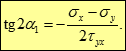
Оскільки тангенс має однакові значення для кутів, що відрізняються один від одного на 1800, отриманий вираз визначає дві площадки, що відрізняються одна від одного на 900. Таким чином, обидві площадки взаємно перпендикулярні. Проте на цих площадках у загальному випадку нормальні напруження перетворюються в нуль. Площадки, на яких дотичні напруження максимальні, називаються площадками зсуву.

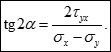
Визначимо кут між площадкою зсуву і головною площадкою. Порівняємо формули для кутів нахилу головних площадок та площадок зсуву:

Оскільки праві частини обернені один одному, то

Таким чином, площадки зсуву повернуті відносно головних площадок на кут 450.

Для визначення величини максимальних дотичних напружень необхідно знайти значення кута через arctg(…) і підставити у вихідний вираз для дотичних напружень, але простіше прийняти у якості вихідного стану головні площадки і перейти до площадок зсуву:

При підстановці кута 1350 або -450 (друга площадка зсуву) отримаємо той же результат, але із оберненим знаком. Таким чином, знову дотримується закон парності дотичних напружень і в загальному випадку можна записати:

Підставимо вирази для головних напружень:

5

• Поняття про круг Мора для напружень.
• Існує графічний спосіб визначення положень головних площадок та напружень, а також напружень на будь-яких інших площадках. Спосіб базується на залежності між нормальними і дотичними напруженнями, що описується рівнянням ІІ порядку, а саме рівнянням круга.

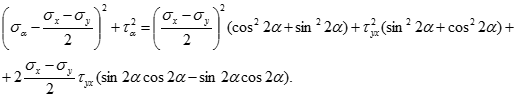
Підведемо до квадрату обидві частини рівнянь для напружень і додамо:

= 1

= 1

= 0

35

Лекція 10 (продовження – 10.4)

• Побудова круга Мора і його використання. Із порівнянь рівнянь координати
• центр круга Мора і радіус рівні:

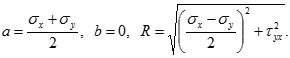
Побудуємо круг Мора для напруженого стану:

 

M

 max

Точка перетину напрямків площадок із колом (точка С) називається полюсом для даного вихідного стану, і визначає напрямок будь-якої похилої площадки, напружений стан якої позначається точкою круга Мора, наприклад, точкою М:

 

B

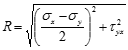
 yx

σ

O

σ

σmin

 xy



 min

Підрахуємо тангенс кута нахилу площадки, що відповідає точці М, до площадки х:

σy

Напружений стан на площадці х характеризується точкою А на кругі напружень.

С

A

σmax

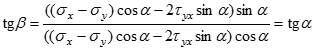
Напружений стан на площадці у характеризується точкою В на кругі напружень.

σx

Таким чином, пряма СМ, що з’єднує показану точку М із полюсом С, показує напрямок похилої площадки, по якій діють напруження σ ,  .

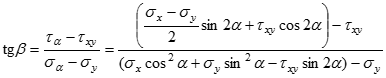
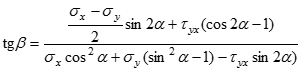
За допомогою круга Мора легко визначаються головні напруження і напрямок головних площадок,

екстремальні дотичні напруження і напрямок площадок зсуву.

36

Лекція 10 (продовження – 10.5)

6