Мультимедійний курс лекцій з опору матеріалів, страница 33

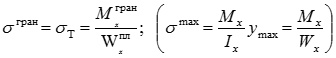
Пластичний момент опору завжди більше моменту опору перерізу в пружній стадії. Наприклад, для прямокутного перерізу:

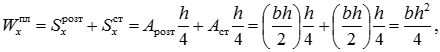
Таким чином, пластичний момент опору прямокутного перерізу в 1,5 рази більше пружного, і це означає, що навантаження може бути збільшене в 1,5 рази з моменту виникнення текучості до повного вичерпання несучої здатності конструкції.

64

Лекція 16

• Внутрішні зусилля при крученні - При крученні в поперечному перерізі стержня виникає лише один силовий фактор - крутний момент Mz. Відповідно до методу перерізів величина і напрямок крутного моменту може бути знайдені з рівняння рівноваги в моментах щодо осі, що збігається з віссю стрижня, складеного для залишеної частини:
• Крутний момент вважається позитивним, якщо при погляді на перетин з боку зовнішньої нормалі він повертає перетин
• по ходу годинникової стрілки.
• Увага! Це правило знаків умовне і не співпадає з прийнятими правилами знаків моментів, кутів повороту в теоретичній механіці і математиці, оскільки пов'язано не з системою координат, а з видом деформації залишеної частини, точно так, як правило знаків для поздовжнього зусилля пов'язано не з напрямком осі z , а з видом деформації розглянутої частини бруса.
• ■ Побудова епюри крутних моментів принципово нічим не відрізняється від побудови епюри поздовжніх сил. Позитивні значення відкладаються нагору від горизонтальної базової лінії, а негативні - вниз.

Нехай прямолінійний брус навантажений зовнішніми зосередженими крутним моментом M1, M2:

1. Реакції лівої опори можна не визначати, тому що в цьому прикладі можна обмежитися розглядом
2. лише сил, прикладених до правих залишених частин (праворуч від перерізів).

Використовуючи отримані вирази для крутного моменту побудуємо епюру крутних моментів: Нехай M1 = 250 Нм, M2 = 100 Нм. Відкладаючи на кожній з ділянок значення крутного моменту в деякому вибраному масштабі отримуємо епюру Mz:

2. Число ділянок - 3

Зверніть увагу, що стрибки на епюрі Mz розташовуються в точках прикладення зовнішніх зосереджених моментів і рівні величинам цих моментів. Відповідно стрибок на лівому кінці епюри дає величину опорного моменту.

3. Проведемо переріз I-I на першій ділянці і визначимо поточну координату перерізу і межі її зміни: 0  z1  a.

4. Відкинемо ліву частину, замінимо її дію крутним моментом MzI-I і складемо рівняння рівноваги в моментах щодо осі z :

MII-II

З рівняння рівноваги отримуємо вираз для крутного моменту на ділянці 1:

Повторюємо кроки 3 та 4 для наступних ділянок:

3. Проведемо переріз II-II на другій ділянці і визначимо поточну координату перерізу і межі її зміни : 0  z2  b.

4. Відкинемо ліву частину, замінимо її дію крутним моментом MzII-II і складемо рівняння рівноваги в моментах щодо осі z :

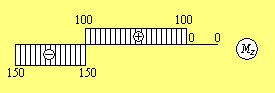
З рівняння рівноваги отримуємо вираз для крутного моменту на ділянці 2:

Аналогічно отримуємо для ділянки 3 (0  z3  c):

Отримані вирази показують, що крутний момент в перерізі дорівнює алгебраїчній сумі моментів зовнішніх сил щодо осі бруса, взятих по одну сторону від перерізу!

Знак доданків позитивний, якщо розглянутий зовнішній крутний момент обертає перетин за годинниковою стрілкою при погляді на переріз з боку зовнішньої нормалі.

65

Лекція 16 (продовження – 16.2)

• Кручення стержнів круглого поперечного перерізу - Кручення характерне тим, що в поперечних перерізах виникають дотичні напруження , що виникають від крутного моменту Mz.

Деформація стержня при крученні виражається тим, що поперечні перерізи повертаються навколо осі стержня z на деякі кути  = (z) , названі кутами закручування.

y

x

• Дотичні напруження при крученні - Як вказувалося раніше, задача
• визначення напружень є статично невизначеною, для вирішення якої
• необхідно послідовно розглянути три сторони задачі:

z

1. Статика: Виділимо малий елемент двома нормальними до осі бруса перерізами і замінимо дію відкинутих частин дотичними напруженнями. Під їх дією елемент знаходиться в рівновазі.