Мультимедійний курс лекцій з опору матеріалів, страница 5

Компоненти напружень по трьом перпендикулярним граням елемента утворюють систему напружень, описувану так званим тензором напружень:

σy

yz

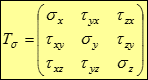
yx

zy

y

Тут перший стовпець представляє компоненти напружень на площадках, нормальних до осі x, другий і третій - до осі y та z відповідно. перший індекс вказує площадку ("місце") дії, другий - напрям. Для нормальних напружень індекси збігаються і один індекс опускається.

xy

Нагадаємо, що опорні реакції конструкції включаються в число зовнішніх сил. Для визначення цих реакцій в статично невизначених системах рівнянь рівноваги недостатньо і слід додатково розглядати переміщення, пов'язані з внутрішніми зусиллями і напруженням, а також фізичні співвідношення пружності. Задача визначення напружень в силу інтегральності співвідношень з внутрішніми Зусиллями, завжди статично невизначена і необхідно додатково розглядати деформації тіла з метою визначення закону розподілу напружень по перерізу.

σz

zx

xz

z

σx

• Зв'язок внутрішніх зусиль і напружень - Внутрішні зусилля в перерізі, як було показано вище,
• пов'язані рівняннями рівноваги з зовнішніми силами, прикладеними до залишеної частини бруса при його перетині. З іншого боку, внутрішні зусилля є результат приведення до центру поперечного перерізу внутрішніх сил, прикладених до елементарних майданчиків (напружень), що виконується додаванням, яке для елементарних сил зводиться до інтегрування за площею поперечного перерізу.

x

y

Виконання цієї операції для кожного з внутрішніх зусиль приводить до наступних інтегральних виразів :

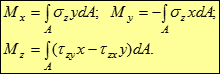
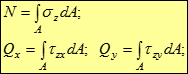
My

zy

Qy

σz

x

Mz

N

zx

Таким чином, в цілому зв'язок зовнішніх сил, внутрішніх зусиль і напружень такий :

z

y

O

Qx

Зовнішні сили

Напруження

Внутрішні зусилля

Mx

Рівняння рівноваги

Інтегральні співвідношення

x

8

Лекція 2 (продовження – 2.2)

• Переміщення – перехід точок тіла в нове положення внаслідок зміни форми і розмірів тіла під дією навантаження.
• Повне переміщення точки в просторі розкладається на компоненти u, v і w, паралельні осям x, y і z, відповідно.
• Переміщення розглядуваної точки залежить від деформації всіх навантажених областей тіла і включає в себе переміщення як жорсткого
• цілого ненавантажених областей. Таким чином, переміщення не може характеризувати ступінь деформування навколо
• розглядуваної точки.
• ■ Деформація в точці - міра деформування матеріалу навколо точки. Виділимо в даній точці тіла елементарний
• об’єм (паралелепіпед зі сторонами dx, dy, dz) і розглянемо його можливі зміни розмірів і форми.

Нехай за рахунок деформації довжини його ребер отримають абсолютні видовження dx, dy та dz:

dy

y

Відносні лінійні деформації в точці :

dy

z

Крім лінійних деформацій, пов'язаних зі зміною розмірів лінійних елементів, виникають кутові деформації або кути зсуву, пов'язані зі зміною форми. Наприклад, у площині xy можуть виникати малі зміни прямих кутів паралелепіпеда :

x

dx

dx

dz

dz

Такі кутові деформації в загальному випадку можуть мати місце у всіх трьох площинах. Всі відносні деформації досить малі і мають для реальних матеріалів порядок ≈10-4-10-3. Таким чином, сукупність відносних лінійних і кутових деформацій визначають деформований стан в точці і утворюють тензор деформацій, подібний тензора напружень: Примітка: Половинні кути зсуву використовуються з метою отримання аналогічних формул перетворення з тензором напружень.

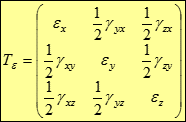
Залежно від того, які з компонент відносних деформацій мають нульове значення в даній області або для всього тіла, розрізняють такі прості види деформацій: 1. Лінійна деформація - εz ≠ 0, кути зсуву дорівнюють нулю, іншими лінійними відносними деформаціями нехтується (Характеризується абсолютним і відносним подовженням). 2. Плоска деформація - εz ≠ 0, εx ≠ 0 або εy ≠ 0, інші відносні деформації дорівнюють нулю (характеризується абсолютним і відносним звуженням площі поперечного перерізу). Ці види деформацій зазвичай реалізуються при розтязі-стиску. 3. Об'ємна деформація - εz ≠ 0, εx ≠ 0, εy ≠ 0, кути зсуву дорівнюють нулю (характеризується абсолютною і відносною зміною об’єму). 4. Чистий зсув - лінійні відносні деформації дорівнюють нулю, кути зсуву не рівні нулю (характеризується зміною форми, зміна об’єму не відбувається). Цей вид деформації також виникає при крученні. Відповідно до виду деформації спочатку послідовно вивчають такі найпростіші напружено-деформовані стани як розтяг-стиск, чистий зсув і кручення, чистий згин. Далі вивчаються більш складні - поперечний згин, складний опір, поздовжній згин.