Приріст згинального моменту і осьовий момент інерції перерізу не залежать від площі відсіченої частини і їх можна винести за знак інтеграла. Залишений підінтегральної вираз співпадає з виразом для статичного моменту площі відсіченої частини поперечного перерізу:
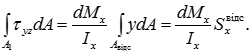
Вважаючи дотичні напруження постійними за площею A1, що відповідає припущенням сталості деформацій зсуву по ширині поперечного перерізу, враховуючи закон парності дотичних переміщень і диференціальну залежність поперечної сили, отримуємо:
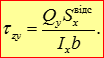
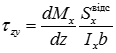
- формула Журавського
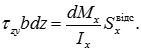
або
59
Лекція 15 (продовження – 15.5)
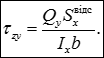
Проведемо горизонтальний переріз на висоті y і обчислимо статичний момент відсіченої частини:
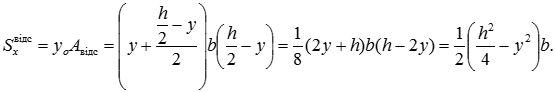
y
Aвідс
yo
y
Підставимо у формулу Журавського вирази для статичного моменту і моменту інерції:
x
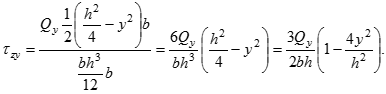
h
Отримана залежність є квадратичною від координати розглянутого шару. Таким чином, дотичні напруження по висоті перерізу змінюються за квадратною параболою: y = h/2, zy = 0; y = 0, zy = zymax =3Qy/(2bh) =1,5 zyср
![]()
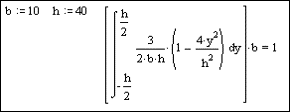
Можна переконатися, що об’єм епюри напружень τzy (y) · b / Qy дорівнює 1, що означає виконання рівності.
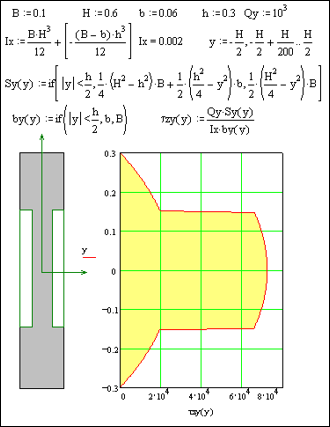
Переріз має ступеневу зміну ширини і тому слід розглядати окремо дві ділянки зміни координати: 0 <y1<h / 2 - стінка і h / 2 <y2<H / 2 - полку.
■ Товстостінний двотавр
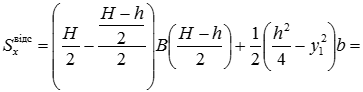
Для стінки:
y2
y1
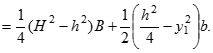
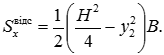
Для полички:
На обох ділянках дотримується квадратична залежність від координати волокна. У місцях різкої зміни ширини перерізу відповідно до формули Журавського епюра має скачки:
60
Лекція 15 (продовження – 15.6)
F
У поличках виникають горизонтальні дотичні напруження zx, які можуть бути визначені за формулою Журавського, при цьому статичний момент площі, що відсікається вертикальною площиною на відстані x1, обчислюється як і раніше відносно осі x:
zx
zx
![]()
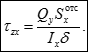
Це випливає з того факту, що при перетині вертикальною площиною в поздовжньому перерізі виникають дотичні напруження xz рівні дотичним напруженням zx в поперечному перерізі на відстані x1. Далі, дотримуючись процедури виведення формули Журавського, приходимо до тієї ж формули.
x1
z0
zy
d
A
На відміну від вище вказаного (визначення вертикальних дотичних напружень), тепер статичний момент відсіченої частини змінюється за лінійним законом:
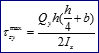
![]()
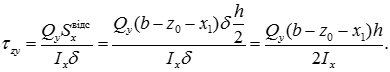
Звідси розглядувані горизонтальні дотичні напруження змінюються також за лінійним законом:
![]()
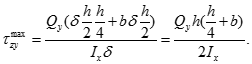
Максимальні дотичні напруження:
![]()
zx
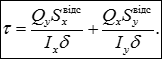
У разі згину одночасно в двох площинах дотичні напруження виходять як алгебраїчна сума:
Перший інтеграл дорівнює площі епюри дотичних напружень τzx, помноженої на товщину полички:
![]()
Умова міцності на зріз: де Rзр – розрахунковий опір матеріалу на зріз.
Таким чином, крутний момент дорівнює
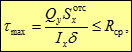
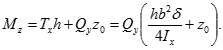
Приведення системи дотичних напружень до рівнодіючої дає:
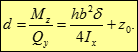
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.