Двовісний напружений стан (стиск)
Для такої спрощеної діаграми граничних напружених станів можливо отримати аналітичну умову міцності з подібності прямокутних трикутників:
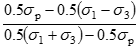
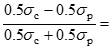
Скоротимо на 0.5 і перемножимо:
![]()
с
р
![]()
3
1
Після скорочення, складання і скорочення на 2 отримаємо:
0.5с
0.5р
![]()
Теорія Мора добре узгоджується з експериментальними даними при σ1> 0, σ3< 0. Недоліком теорії Мора є неврахування проміжного головного напруження σ2.
0.5(3-1)
Звідси співвідношення, яке задовольняє лінії граничних циклів:
0.5с-0.5р
![]()
0.5р
Отже, умова міцності має вигляд:
0.5с
0.5(3+1)
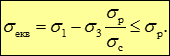
46
Лекція 12 (продовження – 12.4)
■ Критерій пластичного стану - При випробуваннях матеріалів було виявлено, що в пластичному стані максимальне дотичне напруження має одне і те ж значення для даного матеріалу. У результаті, в якості наступної гіпотези переходу матеріалу в граничний стан можна вибрати досягнення найбільших дотичних напружень граничного (небезпечного) значення (критерій пластичності). Ця гіпотеза лягла в основу III теорії міцності. З використанням цього критерію умова міцності має вигляд:
![]()
![]()
У разі плоского напруженого стану:
![]()
![]()
![]()
![]()
При згині з крученням:
Експериментальні дані показують хороший збіг результатів для пластичних матеріалів. Недоліком III теорії, як і вище вказаних теорій, є неврахування середнього головного напруження 2 .
■ IV теорія міцності (енергетична) - Першою спробою зв'язати всі три головні напруження було висунення гіпотези переходу в граничний стан питомої потенційної енергії деформації деякого граничного значення. Експерименти показали, що при всебічному стисканні, пластичні деформації не виникають, хоча при цьому накопичується велика питома потенційна енергія. У зв'язку з цим була висунута гіпотеза про те, що граничний стан обумовлюється досягненням граничного значення лише тієї частини питомої потенційної енергії деформації, яка пов'язана зі зміною форми:
![]()
- повна питома потенційна енергія.
де
![]()
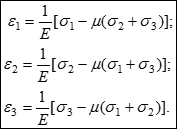
Підстановка узагальненого закону Гука дає такий вираз для повної питомої потенційної енергії:
![]()
Питому потенційну енергію, витрачену на зміну об'єму, можна отримати з цього виразу, приймаючи 1 =2 = 3= о:
![]()
![]()
![]()
Приймемо:
Питома потенційна енергія, що витрачається на зміну форми:
![]()
47
Лекція 12 (продовження – 12.5)
![]()
Отриманий вираз після приведення до спільного знаменника, розкриття квадрата суми, множення і віднімання дає:
![]()
![]()
або
Зауваження: Ці ж співвідношення можна отримати безпосередньо з виразу для повної питомої енергії деформації задаючи по головних площадках напруження, рівні різниці діючих головних напружень і середнього напруження: 1’ = 1 - о, 2’ = 2 - о, 3’ = 3 - о: і підставляючи значення середнього напруження:
![]()
![]()
![]()
Для одноосного розтягування при настанні текучості 1 = Т , 2 = 3 = 0 питома потенційна енергія складає величину:
![]()
Прирівнюючи вирази питомої потенційної енергії зміни форми для тривісного напруженого стану і для одноосного, отримуємо еквівалентне напруження:
![]()
![]()
або
![]()
При згині з крученням:
Як і теорія III, енергетична теорія дає хороший збіг результатів з експериментальними даними для пластичних матеріалів.
■ Поняття про нові теорії міцності та механіки руйнування - Гранична поверхня, відповідна умові появи масових пластичних деформацій і по IV теорії, визначається рівнянням: Рівняння відповідає поверхні кругового циліндра радіуса , вісь якого рівно нахилена до координатних осей 1,2 і 3.
![]()
![]()
Критерій, використаний в ІІІ теорії, дає поверхню правильної шестигранної призми, вписаної в циліндр, тобто гранична область майже співпадає з областю по IV теорії. Критерій найбільших нормальних напружень (І теорія міцності дає куб із ребром рівним о. Новітні теорії міцності ґрунтуються на на виборі різних варіантів граничної поверхні f(1,2, 3) = 0, при якій найбільш повно можливо врахувати особливості опору даного класу матеріалів в умовах складного напруженого стану. Наприклад, у композитних (армованих) матеріалах, руйнування може частково проходити за рахунок розриву волокон, а також частково за рахунок сколювання матриці. У випадку ортотропних матеріалів, що мають різні границі міцності при стиску і розтязі, умова міцності містить константи із відповідних дослідів, тобто використовується не один розрахунковий опір, а два і більше.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.