Мультимедійний курс лекцій з опору матеріалів, страница 13

• Метод руйнуючих навантажень – Оскільки при досягненні в одному із стержнів напружень більше розрахункових (границі текучості) несуча здатність статичної системи не вичерпується, то слід прийняти за небезпечний стан такий, при якому у всіх стержнях, що забезпечують незмінність системи (рівновагу при відсутності будь-яких переміщень) виникають напруження, рівні межі текучості. Для такого стану система перестає бути статично невизначеної, так як тепер відомі зусилля в цих стержнях. Вони дорівнюють добутку поперечної площі перерізу на напруження, рівні межі текучості.
• Все це справедливо при використанні ідеалізованої діаграми розтягування-стиснення (діаграми Прандтля), яка не враховує зміцнення матеріалу після проходження площадки текучості.
• Таким чином, граничне навантаження може бути визначене з умов рівноваги. Очевидно, що таке навантаження не може бути допущене щоб уникнути руйнування системи. Тому його величину ділять на коефіцієнт запасу n, подібно до того, як граничні напруження при пружному розрахунку ділилися на цей коефіцієнт по відношенню до межі міцності або межі текучості.

Умова міцності за методом руйнуючих навантажень при розтягуванні-стисненні стрижнів статично невизначеної системи має вигляд : де

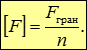
У випадку дії декількох сил передбачається, що сили одночасно збільшуються пропорційно деякого параметру. Тоді знаходиться граничне значення цього параметра, що характеризує граничне навантаження.

• Приклад – Стержень ступінчастого перерізу знаходиться під дією сили F. Ця статично невизначена задача була розглянута і вирішена раніше
• на лекціях. Отримане пружне рішення : max = 0.375F/A. Необхідно визначити
• вантажопідйомність за методом допустимих напружень і методу руйнуючих навантажень.

RA

RB

Умова міцності по допустимим напруженням:

Тоді при Fгран = Fn виникає текучість на першій ділянці, але система може ще сприймати навантаження, тому що на інших ділянках напруження менше Т.

умова міцності по руйнуючим навантаженням:

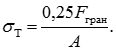
20

Лекція 5 (продовження – 5.3)

Три види розрахунків на міцність при розтягу та стиску Умова міцності при розтязі та стиску

1. Перевірочний розрахунок (перевірка умови міцності): відоме навантаження (поздовжня сила) - N; відомі розміри перерізу (площа поперечного перерізу) – А; відомий матеріал (допустимі напруження) - [σ].

2. Підбір розмірів поперечного перерізу: відоме навантаження (поздовжня сила) - N; відомий матеріал (допустимі напруження) - [σ]; відомий тип площі поперечного перерізу.

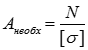
3. Визначення найбільшого допустимого навантаження: відомі розміри перерізу (площа поперечного перерізу) – А; відомий матеріал (допустимі напруження) - [σ].

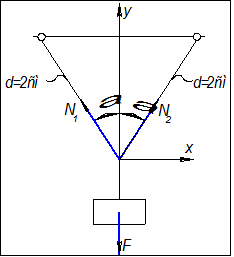
ПРИКЛАД:

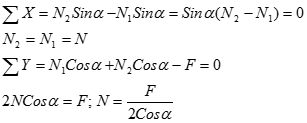
Умова міцності: , , .

21

Лекція 6

• Визначення переміщень при розтязі-стиску. Розглянемо стержень, навантажений розтягуючою силою F. Виділимо на відстані z ділянку довжиною dz. Видовження цієї ділянки dz рівне переміщенню другої її межі щодо першої dw.
• Деформація на цій ділянці визначається виразом,
• і представляє собою диференціальне рівняння:

Розділимо змінні і зведемо рішення цього рівняння до інтегрування лівої і правої частин:

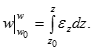
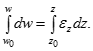
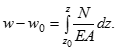
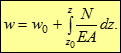
Підставимо межі і вираз для деформації, що слідує із закону Гука :

Тут w0 – переміщення лівої межі аналізованої ділянки на відстані z, EА- жорсткість стержня при розтязі-стиску, N - поздовжня сила.

У разі постійності поздовжньої сили і площі поперечного перерізу маємо:

Звідси, як окремий випадок, отримуємо вираз для абсолютного подовження стержня (w0 = 0, z0 = 0, z = l):

Загальна формула обчислення переміщень показує, що переміщення обчислюються наростаючим підсумком, тобто до переміщення, обчислюваному на даній ділянці [z0, z] (другий доданок), додається переміщення перерізу, відповідного лівій межі, і представляє переміщення всієї ділянки, як жорсткого цілого (твердого тіла). Якщо на кожній з ділянок поздовжнє зусилля і площа поперечного перерізу постійні, то визначення переміщення будь-якого перерізу або кінця стержня зводиться до простого підсумовування видовжень кожного з ділянок від нерухомого перерізу до розглянутого.