Мультимедійний курс лекцій з опору матеріалів, страница 28

У загальному випадку балка може підлягати згину під дією згинальних моментів щодо осей x і y. Якщо один з них дорівнює нулю, а інший лежить у головній площині перерізу (площині, що проходить через вісь стержня і одну з головних центральних осей інерції), то такий згин називається плоским згином. Якщо при цьому згинальний момент постійний, і це означає відсутність поперечної сили, то такий вигин називається чистим згином.

z

Підставимо напруження у вираз для згинального моменту (y0  y ) :

• Нормальні напруження при чистому згині - Як вказувалося раніше, задача визначення напружень є статично
• невизначеною, для вирішення якої необхідно послідовно розглянути три сторони задачі:

= Ix

1. Статика: Виділимо малий елемент двома нормальними до осі бруса перерізами і замінимо дію відкинутих частин нормальними напруженнями. Під їх дією елемент знаходиться в рівновазі.

A

Вище приведенням розподілених сил до центру і центральних осей було отримано інтегральні співвідношення, що зв'язують нормальні зусилля і згинальний момент з нормальними напруженнями:

Так як нормальні зусилля при згині дорівнює нулю, то:

Зауваження: Знак мінус враховує правило знаків для згинального моменту і напружень.

Останнє судження вказує на те, що в перерізі виникають напруження різного знаку і слід припускати, що існують волокна, в яких напруження дорівнюють нулю (нейтральна вісь).

z

З цих співвідношень знайти напруження і положення нейтральної осі поки не можна, оскільки закон зміни напружень по висоті перерізу невідомий.

zdA

2. Геометрія: Відповідно до гіпотези плоских перерізів, поздовжні волокна отримують деформації розтягування-стиснення, пропорційні відстані від нейтральної осі. Нейтральна вісь, як і центральна вісь стрижня, вигинається і має радіус кривизни  (т. А – центр кривизни).

+

y

Mx

z

z0

z

Абсолютне видовження волокна, що знаходиться на довільній відстані від нейтральної осі, з подоби трикутників дорівнює:

–

Таким чином, нормальні напруження лінійно залежать від відстані до нейтральної осі. При y0 > 0 – стиск.

3. Фізика: По закону Гука:

Підставимо зусилля у вираз для нормальної сили:

Цей інтеграл являє собою статичний момент площі і рівність його нулю означає, що нейтральна вісь проходить через центр ваги.

56

Лекція 15 (продовження – 15.2)

• Момент опору при згині - З формули напружень при згині випливає, що найбільші (позитивні - розтягуючі) і найменші (негативні – стискаючі) напруження в поперечному перерізі виникають в точках, найбільш віддалених від нейтральної осі, розташованих по обидві сторони від неї:
• При симетричному перерізі відносно нейтральної осі
• абсолютні величини найбільших розтягуючих і стискаючих напружень
• рівні і можуть бути визначені за формулою: В інших випадках необхідно спеціально шукати ymax , але формула залишається вірною.

Величина, що залежить тільки від розмірів і форми поперечного перерізу, називається осьовим моментом опору:

З використанням осьового моменту опору максимальні напруження обчислюються як:

Моментом опору зручно користуватися при розрахунку на міцність (підборі перерізу) балки при згині. Звичайно, для цього моменти опору попередньо обчислюються для типових і прокатних перерізів за попередньою формулою.

• Момент опору типових і прокатних перерізів:
• 1. Прямокутний переріз:

2. Круглий переріз:

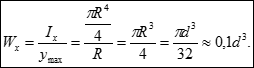
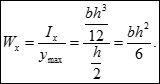
3. Для прокатних перерізів всі геометричні характеристики, в тому числі і моменти опору, вже обчислені та зібрані до спеціальних таблиць - сортаменту.

У всіх випадках, крім круглого перерізу, потрібно використовувати моменти опору, відповідні орієнтації площини дії згинального моменту. Наприклад, при дії на балку прямокутного перерізу моменту My при обчисленні максимальних нормальних напружень необхідно використовувати Wy:

• Умова міцності по нормальним напруженням:

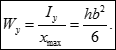
Максимальні напруження не повинні перевищувати розрахункових або допустимих напружень.