Мультимедійний курс лекцій з опору матеріалів, страница 16

26

Лекція 8

y

v

• Залежність між моментами інерції при повороті осей

dA

x

u

Координати елементарної площадки dA в системі координат u, v виражаються через вихідні координати x, y лінійними залежностями:

v

u

ycos



y

xcos

Осьові моменти інерції щодо осей u і v:

xsin



x

O1

ysin

x

Сума осьових моментів інерції щодо двох перпендикулярних осей не залежить від кута  і при повороті осей зберігає постійне значення.

Відцентровий момент інерції щодо осей u і v:

• Головні осі та головні моменти інерції - Отримані залежності
• показують, що при зміні кута повороту осей значення моментів інерції змінюються,
• при цьому сума осьових моментів інерції залишається постійною.
• Це означає, що можна визначити таке положення осей, при якому один з осьових моментів
• досягає максимального значення, а інший - відповідно мінімального значення:

Максимальні та мінімальні осьові моменти інерції називаються головними моментами інерції, а осі, щодо яких вони обчислюються, - головними осями. Для визначення положення головних осей досить прирівняти до нуля першу похідну осьового моменту інерції по куту повороту:

Отриманий результат показує, що для шуканого положення осей відцентровий момент перетворюється в нуль.

Звідси ж слідує:

Оскільки тангенс має однакові значення для кутів, що відрізняються один від одного на 1800, отриманий вираз визначає два положення осей, що відрізняються один від одного на 900. Таким чином, обидві головні осі взаємно перпендикулярні.

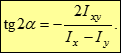
27

Лекція 8 (продовження – 8.2)

Для визначення величини максимальних і мінімальних моментів інерції (головних моментів інерції) треба знайти значення кута через arctg(.) і підставити у вихідний вираз для осьових моментів інерції, або безпосередньо використовувати тригонометричні формули подвійних кутів, як це було зроблено, наприклад, при визначенні головних напружень. Тут зробимо трохи інакше. Представимо осьовий момент у вигляді:

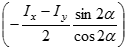
Підставляючи останній вираз і скорочуючи різницю моментів інерції отримуємо остаточно:

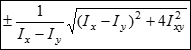
Знак плюс перед другим доданком відноситься до максимального моменту, знак мінус - до мінімального.

• Зауваження. Отримані формули для моментів інерції,
• пов'язані з поворотом осей, а також для головних моментів
• інерції, практично аналогічні по структурі
• відповідних формул для нормальних і дотичних
• напружень на похилих майданчиках і для головних
• напружень. Звідси можна зробити висновок, що положення
• осей, відповідних екстремальним значенням моментів
• інерції і самі значення можна знаходити за допомогою
• кола Мора, побудованого для моментів інерції.

Iu

Iv

Imax

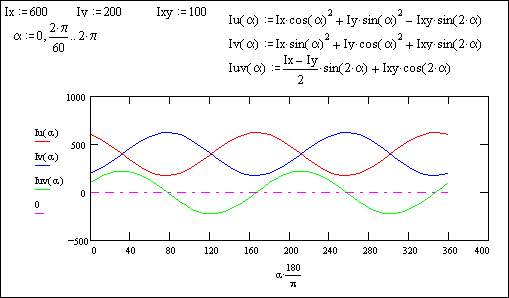
Тут же проілюструємо характер зміни моментів інерції при послідовному повороті осей в діапазоні 0 – 2 π (графіки побудовані в системі MathCAD): Добре видно, що при досягненні осьовими моментами інерції максимальних і мінімальних значень відцентровий момент інерції обертається в нуль. А при досягненні відцентровим моментом інерції максимального значення (при повороті від головних осей на 45 о ) осьові моменти стають рівними між собою.

Imin

Iuv

28

Лекція 8 (продовження – 8.3)

• Радіус інерції - є величина, що зв'язує момент інерції з площею поперечного перерізу і визначається з рівності:
• Радіус інерції являє собою відстань від розглянутої осі до тієї точки, в якій умовно можна зосередити
• всю площу поперечного перерізу. Ця величина характеризує наскільки добре "розвинений" переріз, як далеко знаходяться від осі
• окремі області перерізу, що в свою чергу характеризує економічність перерізу при згині і стиску із згином.

Радіусом інерції зручно користуватися при оцінці гнучкості стиснутих стержнів. Звичайно для цього радіуси інерції попередньо обчислюються для типових і прокатних перерізів за формулами:

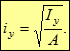
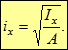
Радіуси інерції, відповідні головним осях, називаються головними радіусами інерції і визначаються за формулами: