Мультимедійний курс лекцій з опору матеріалів, страница 27

Виділений елемент знаходиться в рівновазі і задовольняє рівняння рівноваги:

З першого рівняння отримуємо: Похідна від поперечної сили по поздовжній координаті дорівнює інтенсивності розподіленого навантаження.

З другого рівняння, нехтуючи значеннями другого порядку малості отримуємо: Похідна від згинального моменту по поздовжній координаті дорівнює поперечної силі.

54

Лекція 14 (продовження – 14.3)

• Побудова епюр згинаючих моментів і поперечних сил - принципово нічим не відрізняється від побудови епюри поздовжніх сил і крутних моментів. Позитивні значення поперечної сили Qy відкладаються нагору від горизонтальної базової лінії, а негативні - вниз. Позитивні значення згинальних моментів Mz відкладаються вгору - з боку стиснутого волокна. Таким чином розташування ординат епюри Mz вказують, які волокна стиснуті.
• Примітка: Це правило прийнято в машинобудівних та авіаційних вузах, у той час, як в будівельних і транспортних вузах використовується зворотне правило (позитивний момент відкладається з боку розтягнутого волокна).

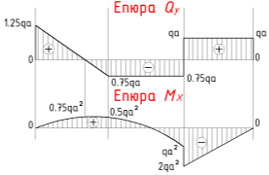
Використовуючи отримані вирази для поперечної сили і згинального моменту побудуємо епюру поперечних сил і згинальних моментів, підставляючи значення реакцій і координати початку і кінця ділянок. У разі квадратичної зміни величини (згинальний момент на першій ділянці) додатково підставляється координата точки всередині інтервалу, наприклад, посередині. Відкладаючи на кожній з ділянці значення поперечних сил і згинального моменту в деякому вибраному масштабі отримуємо епюри Qy і Mx:

Нехай балка навантажена рівномірно розподіленим навантаженням q, зосередженої силою F = qa і обертовим моментом M=qa2:

y

1. визначаємо опорні реакції :

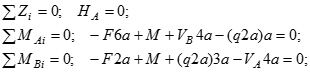
q

F

M

HA

A

VB = 1,75qa

B

z

VA

VA = 1,25qa

VB

2 кількість ділянок– 3.

Із другого та третього рівняння отримуємо:

3. Проведемо переріз І-І на першій ділянці та визначимо поточну координату перерізу та межі її зміни: 0  z1  2a.

y

4. Відкинемо праву частину, замінивши її дію поперечною силою QyI-I та згинаючим моментом MxI-I та складемо рівняння рівноваги в проекціях і в моментах відносно вісі х, що проходить через центр поточного перерізу (тобто відносно точки С):

Виконуємо контроль:

Звідси отримуємо :

Властивості епюр: 1. Рівномірно розподілене навантаження на ділянці своєї дії викликає на епюрі Q похилу пряму лінію, спадаючу в сторону дії навантаження, а на епюрі M - параболу з опуклістю проти дії навантаження. 2. Зосереджена сила викликає на епюрі Q стрибок в точці прикладання сили в бік дії сили, а на епюрі М - перелом проти дії навантаження. 3. Зосереджений момент не викликає на епюрі Q в точці його програми ніяких особливостей, а на епюрі M викликає стрибок. Дивіться і дивуйтеся!

Повторюємо кроки 3 та 4 для наступних ділянок :

3. Проведемо переріз II-II на другій ділянці і визначимо поточну координату перерізу і межі її зміни : 0  z2  2a.

4. Відкинемо праву частину, замінимо її дію поперечної силою QyII-II і згинаючим моментом MzII-II і складемо рівняння рівноваги в проекціях і в моментах щодо осі x, що проходить через центр поточного перерізу (тобто відносно точки D):

Звідси отримуємо:

Аналогічно отримуємо для ділянки 3 (0  z3  2a):

55

Лекція 15

• Згин балок. Основні припущення:
• Поздовжні волокна стержня (паралельні його осі) отримують лише деформації розтягування-стиснення
• і не здійснюють тиску один на одного (гіпотеза про відсутність тиску поздовжніх волокон один на одного).

Mx

Mx

2. Кожний поперечний переріз стержня, плоский до деформацій, залишається плоским і нормальним до деформованої осі стержня після деформації (гіпотеза плоских перерізів).

z

Перша гіпотеза нехтує впливом нормальних напружень σx і σy на поздовжню деформацію елемента, друга - деформаціями зсуву. Обидві гіпотези підтверджуються експериментально на основній частині довжини стрижня.