Мультимедійний курс лекцій з опору матеріалів, страница 36

3. Геометрія: Складаємо рівняння сумісності деформацій :

RB

Це рівняння встановлює незмінність загальної довжини стержня при будь-яких діях, яку забезпечували зв'язки (жорсткі закріплення) до їх видалення.

4. Фізика: Записуємо співвідношення зв'язку деформацій з зусиллями :

Отримали повну систему рівнянь, що вирішує дану задачу (5 рівнянь та 5 невідомих - 2 реакції і 3 переміщення).

Підставляємо співвідношення пружності в рівняння сумісності:

Підставимо отримане співвідношення в рівняння рівноваги:

Такий же результат можна отримати з використанням статично визначеної системи, утвореної з заданої статично невизначеної відкиданням “зайвого" зв'язку, та принципу незалежності дії сил:

Складаємо рівняння сумісності деформацій :

або

Це рівняння встановлює незмінність загальної довжини, яку забезпечував зайвий зв’язок (праве жорстке закріплення) до її видалення, або рівність переміщень та їх протилежний напрямок при окремій дії зовнішнього навантаження та реакції цього зв’язку.

Якщо був наявний початковий зазор, наприклад між правим кінцем стержня і закріпленням, або навпаки натяг (початковий розмір стержня перевищував відстань між опорами), то це враховується лише в рівняннях сумісності деформацій : або (>0 зазор, <0 натяг)

Записуємо відношення зв’язку деформацій (переміщень) із зусиллями:

Епюра нормальних напружень також будується обчисленням значень напружень по ділянках : σ1 = N1 / A1= 3F/8A, σ2 = N2 / A2= F/8A, σ3 = N3 / A3= F/4A. У перерізі різкої зміни площі отримали стрибок.

Отримали повну систему рівнянь, що вирішує дану задачу (4 рівняння та 4 невідомих – 2 реакції та 2 переміщення).

Підставимо отримане співвідношення у рівняння рівноваги та отримаємо величину іншої опорної реакції (RB).

Якщо замість силового навантаження, або додатково до нього, діє температурне навантаження (нагрів), то це враховується введенням температурних видовжень в рівняння спільності деформацій.

Підставляючи переміщення у рівняння сумісності:

71

Лекція 18 (продовження – 18.2)

• Розрахунок статично невизначених систем на дію температури – У статично невизначених системах нагрівання (охолодження) елементів викликає додаткові внутрішні зусилля (напруження), які можуть значно перевищувати зусилля від дії силового навантаження. Загальний порядок вирішення завдання зберігається, але рівняння сумісності деформацій (видовжень) містять видовження від дії різниці температур t :  - коефіцієнт лінійного розширення матеріалу, l - довжина стрижня.
• Приклад 2. Стержень змінного перерізу (2A і A), розглянутий у прикладі 1, додатково нагрівається на t градусів.
• t

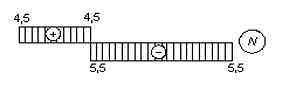
1. Вибираємо об'єкт рівноваги, відкидаємо зв'язки і замінюємо їх дію реакціями:

RA

RB

2. Статика : Складаємо рівняння рівноваги:

3. Геометрія: Складаємо рівняння сумісності деформацій :

Це рівняння встановлює незмінність загальної довжини стержня при будь-яких діях, у тому числі від нагріву, яку забезпечували зв'язки (жорсткі закріплення) до їх видалення.

4. Фізика: Записуємо співвідношення зв'язку деформацій з зусиллями і температурних впливом :

Підставляємо співвідношення пружності і температурного видовження в рівняння сумісності:

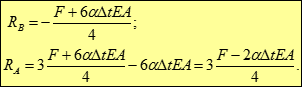
Підставимо отримане співвідношення в рівняння рівноваги:

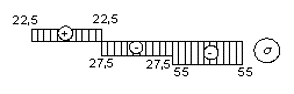
При відсутності нагріву значення напружень виходять рівними 37.5 МПа, - 12.5 МПа, і -25 МПа відповідно (вид епюри напружень див. у прикладі 1). Таким чином, нагрів всього на 10о привів до збільшення стискаючої сили і максимальних стискаючих напружень більше, ніж в 2 рази. Статично невизначені системи завжди реагують на зміну температури зміною внутрішніх зусиль. Це ж відбувається при взаємних зсувах опор (нерівномірне осідання опор).

Тепер, при температурному впливі, у вирази для реакцій входять абсолютні значення модуля пружності E і площі A. Обчислимо величини реакцій для конкретних даних: F = 10 кН, A = 1 см2, t = 10o, E = 2*105 МПа,  =10-5 (сталь):