Таким чином, врахування рівномірно розподіленого поздовжнього навантаження (власної ваги) може бути виконано безпосереднім інтегруванням по розглядуваній ділянці або використанням виразу, подібного абсолютному видовження стержня при постійній поздовжній силі, в якому сила зменшена удвічі! (див. результат визначення переміщення кінця стержня).
Наприклад, другий результат (переміщення перерізу посередині довжини стержня) може бути отриманий, як сума переміщень розглянутого перерізу стержня від дії власної ваги верхньої частини, враховуваного як розподілене навантаження, і переміщення його від ваги нижньої частини, діючого на верхню частину як зовнішня сила:
Поздовжнє зусилля від власної ваги в довільному перерізі на відстані z дорівнює вазі нижчерозташованої частини стержня і лінійно залежить від координати. Епюри поздовжньої сили і нормальних напружень мають вигляд трикутників:
![]()
Переміщення будь-якого перерізу на відстані z має квадратну залежність від координати:
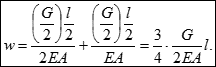
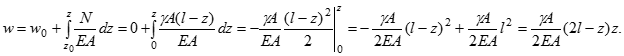
Визначимо переміщення кінця стержня і перерізу на відстані половини довжини :
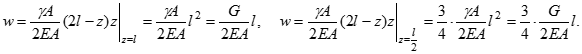
Тут G - вага стержня.
22
Лекція 6 (продовження – 6.2)
Призматичний брус
Поздовжня сила у перерізі І-І на відстані z:
![]()
Згідно умови міцності при розтязі-стиску:
![]()
![]()
Звідки:
![]()
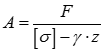
![]()
Із врахуванням всієї довжини стержня l, матимемо:
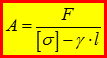
- підбір перерізу призматичного брусу з врахуванням власної ваги.
Напруження тільки від власної ваги стержня
Поздовжня сила у перерізі І-І на відстані z:
![]()
Згідно умови міцності при розтязі-стиску:
![]()
Тоді максимальні напруження тільки від власної ваги стержня будуть рівні:
![]()
Лекція 6 (продовження – 6.3)
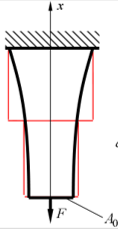
Брусом рівного опору називається брус, у якому напруження за довжиною не змінюються і, як правило, дорівнюють допустимим напруженням.
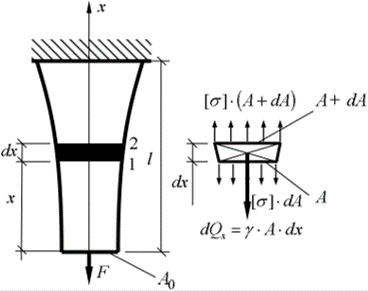
Умова рівноваги знизу ділянки dx (переріз 1):
![]()
Умова рівноваги зверху ділянки dx (переріз 2):
![]()
Віднявши ці два рівняння, отримаємо:
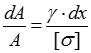
![]()
або
![]()
Проінтегруємо ліву і праву частини отриманої рівності:
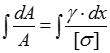
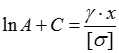
Знайдемо сталу інтегрування С:
![]()
![]()
![]()
При х = 0,
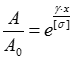
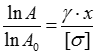
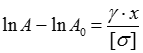
Із знайденою сталою інтегрування С:
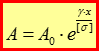
Звідки
- формула підбору перерізу брусу рівного опору при розтязі або стиску.
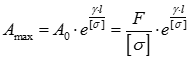
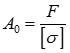
Максимальне значення необхідної площі:
, де
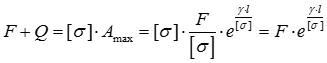
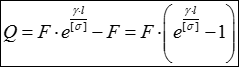
Вага брусу рівного опору
23
Для спрощення розрахунку та виготовлення, брус рівного опору замінюють ступінчастим брусом.
Лекція 6 (продовження – 6.4)
Ступінчастий брус
Визначимо необхідну площу поперечного перерізу кожної ділянки брусу.
Розглянемо нижню частину брусу довжиною l1:
![]()
![]()

Розглянемо середню частину брусу довжиною l2:
![]()
![]()

Розглянемо верхню частину брусу довжиною l3:
![]()
![]()

Лекція 6 (продовження – 6.5)
Деформації від власної ваги
Виріжемо на брусі полосу довжиною dz на відстані z від нижнього кінця брусу.
Деформації видовження полоси від власної ваги частини брусу довжиною z, що знаходиться нижче перерізу, знаходимо згідно закону Гука в розгорнотому вигляді:
![]()
де
- поздовжня сила в перерізі;
![]()
- довжина ділянки;
![]()
![]()
звідки
Визначимо деформації всього брусу від власної ваги:
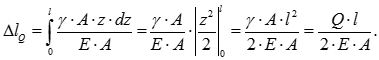
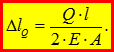
Таким чином деформації від власної ваги брусу
Деформації брусу рівного опору від власної ваги:
![]()
![]()
так як
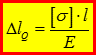
- абсолютні деформації брусу рівного опору.
![]()
![]()
Лекція 7
![]()
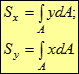
yC
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.