Товарное хозяйство – нелинейная динамическая система, страница 41

Взаимно дополнительными величинами являются координата частицы и ее скорость (импульс), энергия и время и др. Состояния, в которых взаимно дополнительные величины одновременно имеют точные значения, принципиально невозможны. Если одна из них абсолютно точно определена, то значение другой является абсолютно неопределенным.

В том же 1927 г. Вернером Гейзенбергом установлен принцип неопределенности для частиц квантового мира - характеризующие физическую систему дополнительные величины не могут одновременно принимать точные значения. Он  отражает двойственную, корпускулярно-волновую природу элементарных частиц материи:

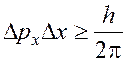
где - импульс;  - координата; h- постоянная Планка.

Принцип неопределенности Гейзенберга (фундаментальное положение квантовой теории) является частным случаем принципа дополнительности Бора.

Оба принципа не ограничивают, как считали первоначально, познание реальной действительности, а лишь указывает на степень применимости к ней понятий и законов классической механики (макроскопических характеристик).

Очевидно, что невозможность точного определения какой-то величины в определенных условиях современная наука не связывает с потерей науки статуса «строгая наука». Никто физику после открытия принципа дополнительности Бора и принципа неопределенности Гейзенберга не перестал считать «строгой наукой».

«Горизонт предсказуемости» в современной точной науке

Экономика является системой с обратной связью и ограниченными ресурсами, нелинейной динамической системой. Простейшим уравнением, описывающим такого рода системы является дифференциальное логистическое уравнение  или его итерационный аналог , анализ которых проведен при рассмотрении темы 3 («Химические модели в экономике»).

При увеличении константы скорости процесса rсистема изменяет характер своего поведения, последовательно переходя от состояния с постоянной скоростью процесса (r меньше 2), к автоколебательному режиму изменения скоростей процесса (с удвоением периодов колебаний) (r больше 2, но меньше 2,57), а затем сначала к «детерминированному хаосу с окнами устойчивости» (r равно 2,57, но меньше 3) и, наконец, к полному «детерминированному хаосу» в режиме изменения скоростей (r равно или больше 3)  (рис. 8.2). «Хаотический» режим означает наличие «горизонта предсказуемости» (в традиционном смысле) событий в системе, но не означает ликвидацию причинности событий, так как процесс полностью воспроизводим!

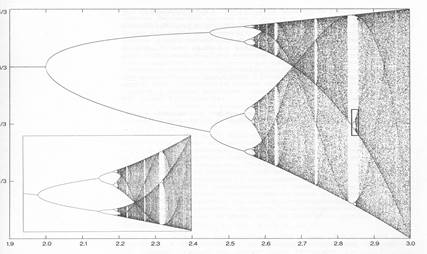
Рис. 8.2 Бифуркационная диаграмма – зависимость  (ось ординат) от r(ось абсцисс). Горизонт предсказуемости (r =3).

Получается на первый взгляд парадоксальная ситуация: система описывается уравнением, причем простейшим уравнением, то есть является детерминированной (вполне определенной), а ее поведение оказывается при некоторых значениях управляющего ею параметра «непредсказуемым» в традиционном смысле, то есть его невозможно определить аналитическими методами. Тем не менее, положение системы можно, если хватит ресурса, определить численным (вычислительным) экспериментом. Открытие точными науками «горизонта предсказуемости» событий – величайшее научное достижение. Это фактически проблема предельных ситуаций, перехода количества в новое качество.

Мультимодальность (мультистабильность) состояний системы

При анализе нелинейных динамических систем, в том числе товарно-денежного хозяйства, их уравнений состояния и фазовых диаграмм (темы 1,2,3,4) было показано, что при одном и том же значении полной (кинетической и потенциальной) энергии системы могут быть реализованы несколько ее стационарных состояний устойчивого и неустойчивого равновесия (имеет место мультимодальность или мультистабильность стационарных состояний или, иначе говоря, равновозможность их существования). Отбор этих состояния в природных системах осуществляется окружающей средой (внешними для системы параметрами). Для социально-экономической системы как нелинейной динамической системы многих частиц («частицы» – хозяйствующие объекты) выбор может быть осуществлен ее «частицами» - хозяйствующими субъектами.