Товарное хозяйство – нелинейная динамическая система, страница 16

Уравнение Мальтуса – это фактически открытое и используемое в биологии (обществе) химическое уравнение, вытекающее из закона действующих масс (см. тему 3). Оно применимо не только к численности популяции, но также и к процессу производства любых жизненных благ. Это еще раз свидетельствует о том, что законы химии выполняются в биологии.

4.3. Модель с ограниченным размножением

Особи популяции не только рождаются, но и умирают. Поэтому уравнение динамики популяции следует переписать в виде:

    ,

где    – коэффициент смертности,    – коэффициент прироста популяции, x – N (численность популяции), x₀ – N₀ (исходная численность популяции).

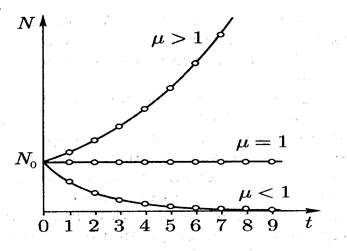
Рис. 4.1. Динамика численности популяции при различных коэффициентах ее прироста.

4.4. Модель Ферхюльста (с ограниченным ресурсом)

Модель Ферхюльста учитывает то обстоятельство, что коэффициент прироста («размножения») уменьшается с увеличением численности популяции, что связывается с ограничением какого-либо ресурса (например, продуктов питания). Эта модель описывается дифференциальным уравнением:

или соответствующим ему итерационным отображением (так называемая «логистическая модель»):

.

Эти уравнения также являются уравнениями, вытекающими из закона действующих масс, то есть химическими по своей природе уравнениями, которые выполняются в биологии (см. тему 3). Их графические решения представлены на рис. 4.2 и рис. 4.3.

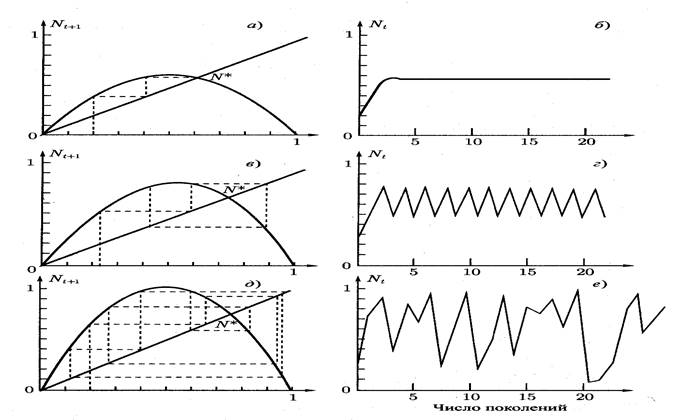
Рис. 4.2 Монотонное приближение к равновесию (а,б); цикл 2 (в,г), детерминированный хаос (д,е).

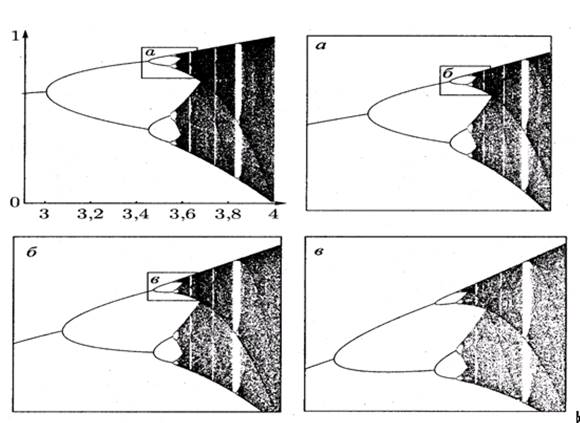
Рис. 4.3 Бифуркационная диаграмма, самоподобие структуры

(ось абсцисс - r)

В зависимости от значений константы скорости процесса r имеет место несколько сценариев: популяция может вырождаться; достигать постоянной численности; возможны гармонические колебания ее численности, включая удвоения периодов колебаний; детерминированный хаос. 

4.5. Модель с двойным ограничением:

где   x(t)  – численность популяции в момент времени t,  – коэффициент рождаемости,  – коэффициент смертности, вызванной старением организма,  – коэффициент смертности, связанный с ограничением ресурса.

При    численность популяции стремится к нулю (популяция вымирает).

При  численность популяции с увеличением времени стремится к устойчивому стационарному значению (режиму). 

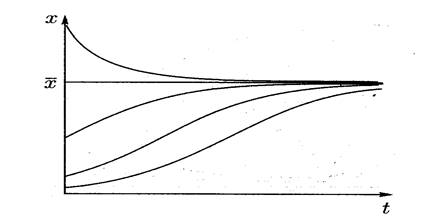
Рис. 4.4 Динамика решений логистического уравнения с двойным ограничением

4.6. Модель Лотка-Вольтерра (хищник-жертва):

Первая математическая модель, описывающая динамику взаимодействующих популяций, появилась в 20-х годах ХХ века – модель Лотка-Вольтерра: 

 –  плотность популяции жертвы и хищника соответственно (желающие могут считать, как отмечает академик Арнольд В.И., что жертвы – это трудящиеся, а хищники – это организованные преступники [1]);

  – скорость размножения популяции жертвы в отсутствии хищника, удельная скорость потребления популяцией хищника популяции жертвы при единичной плотности обеих популяций,

 – естественная смертность хищника,  – коэффициент переработки потребленной хищником биомассы жертвы в собственную биомассу. 

В основу модели положены следующие идеализированные представления о характере внутривидовых и межвидовых отношений в системе «хищник-жертва»:

1. В отсутствии хищника популяция жертвы размножается в соответствии с принципом Мальтуса – экспоненциально;

2. Популяция хищника в отсутствии жертвы вымирает;

3. Суммарное количество жертвы, потребленное популяцией хищника в единицу времени, линейно зависит и от плотности популяции жертвы, и от плотности популяции хищника;

4. Потребленная хищником биомасса жертвы с постоянным коэффициентом перерабатывается в биомассу хищника;

5. Какие бы то ни было дополнительные факторы, оказывающее влияние на динамику популяций, отсутствуют.

В условиях изоляции   численность жертв экспоненциально возрастает   , а численность хищников экспоненциально убывает    

При взаимодействии  в системе может наблюдаться равновесное состояние, отвечающее стационарному решению: