Товарное хозяйство – нелинейная динамическая система

ТЕМА  1: «ТОВАРНОЕ ХОЗЯЙСТВО – НЕЛИНЕЙНАЯ ДИНАМИЧЕСКАЯ СИСТЕМА»

Содержание темы

1.  Динамические системы.

2.  Линейные и нелинейные системы.

3.  «Флаги» нелинейных систем.

4.  Товарное хозяйство как нелинейная динамическая система.

5.  Вопросы для самоконтроля.

6.  Литература к теме 1.

1.1. Динамические системы

В математике в общем случае объект или процесс описывается определенной в пространстве R^N с координатами  системой n интегро-дифференциальных уравнений

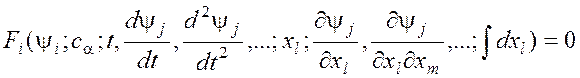, (1)

где  , , , . Переменные  x_l  и tрассматриваются как пространственные и временные координаты. Система уравнений (1) – множество (нелинейных) уравнений в частных производных. Решения уравнений  называются переменными состояния. Предполагается, что уравнения  зависят отпараметров , называемых управляющими параметрами, так как они могут качественно влиять на свойства решений .

Решение системы этих уравнений является сложной задачей  и поэтому ее упрощают, ограничиваясь, во-первых, системой уравнений в частных производных, не содержащих пространственных производных, во-вторых,  предполагая, что она не зависит от пространственных координат, и, наконец, считая, что она содержит производные по времени не выше первого порядка, которые входят в упрощенную функцию  специальным («каноническим») образом.

Систему уравнений: 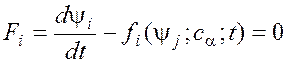 (2), где функции  f_i во многом аналогичны компонентам силы в классической механике, называют динамической системой.

Если функции  f_i в уравнениях (2) не зависят от времени, то такая система называется автономной динамической системой:

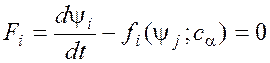
В случае консервативной системы (

функции f_i могут быть заданы антиградиентом потенциальной функции) возможно значительное упрощение системы уравнений:

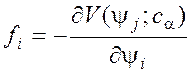
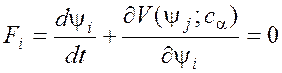,  (3)

Эту систему называют градиентной (потенциальной) динамической системой.

Наибольший интерес представляет изучение состояний равновесия градиентных систем:

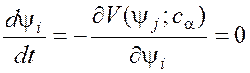, (4)

Именно такого рода динамические системы в основном изучаются в настоящее время. Динамические системы многих частиц, в которых потенциальная энергия не полностью переходит в кинетическую энергию, являются «вязкими» системами, в которых пропорциональна приложенной силе скорость движения частицы (системы Аристотеля), а не ее ускорение (системы Ньютона).

Все реальные системы являются нелинейными. Во многих случаях нелинейные системы можно отобразить линейными моделями, для чего используются методы линейной апроксимации (линеаризации).

Линейные зависимости и функции

Линейная зависимость – это соотношение вида:

,

где  a₁, a₂, …a_n   – числа, из которых хотя бы одно отлично от нуля; x₁, x₂, …x_n  – те или иные математические объекты, для которых определены операции сложения и умножения на число. Термин «линейная зависимость» объясняется тем, что величины  x₁, x₂, …x_n   входят в уравнение в 1-й степени (линейно).

Линейная функция – функция вида  (приращение функции пропорционально приращению аргумента, график функции – прямая линия, наклон которой характеризует коэффициент a).

Нелинейные зависимости и функции

Нелинейность, нелинейная функция – термины, относящиеся к зависимостям, графики которых не являются прямыми линиями.

Геометрический образ нелинейной функции – кривая на плоскости, искривленная поверхность в трехмерном пространстве или более сложные многообразия в пространстве большего числа измерений.

Однако разграничение линейных и нелинейных теорий,  систем  и моделей принято проводить по другому признаку, а именно по типу описывающих их дифференциальных уравнений.

1.2. Линейные и нелинейные системы

Линейная система – это система, движения которой описываются линейными дифференциальными уравнениями.

Например, колебания гармонического осциллятора (например, маятника) описываются синусоидой – нелинейной функцией, но удовлетворяют линейному дифференциальному уравнению , поэтому теорию гармонического осциллятора считают линейной.

Нелинейная система – система, описываемая нелинейными дифференциальными уравнениями.

Нелинейные динамические системы

Раньше считали, что только линейные теории описывают сущность реального мира, что именно они дают главный вклад в бесконечный ряд приближений к истине, определяют лицо истины, а нелинейностям отводили роль косметики на «прекрасном лике» линейной теории. В действительности все оказалось не так.

Все нелинейные дифференциальные уравнения имеют несколько решений (корней, радикалов) и, соответственно, все описываемые ими системы имеют несколько стационарных (установившихся) состояний, а протекающие в них процессы являются ветвящимися процессами.

В нелинейных системах не выполняется принцип суперпозиции – простого сложения откликов системы на внешние воздействия, для них характерен синергизм – отклик на совместное действие факторов отличается от суммы откликов при действии этих факторов порознь.

В нелинейных системах наблюдаются качественные, в том числе скачкообразные изменения свойств, при плавном изменении величины воздействующих  на них факторов.