Товарное хозяйство – нелинейная динамическая система, страница 14

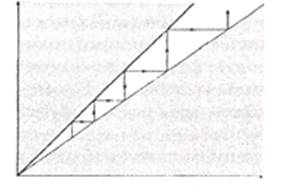
Рис. 3.1

В случае автокаталитической реакции с ограниченным ресурсом (А-Х):

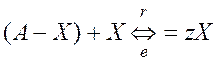
скорость прямой реакции описывается нелинейным (квадратичным) дифференциальным уравнением

.

Это дифференциальное уравнение также можно превратить в итерационное уравнение (с дискретным временем)

.

В этом случае зависимость  от  описывается параболой (рис. 3.2, 3.3, 3.5, 3.8), высота которой определяется r. Дискретная динамика кумулятивного процесса изменения Х, будет описывать уравнение . При  меньше  (биссектриса) процесс затухает (рис. 3.2).

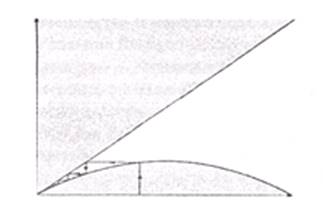
Рис. 3.2.

Анализ отображений  выполнил Фейгенбаум, выявив универсальные закономерности в поведении такого рода систем. При 0 < r< 2 анализируемая величина постепенно возрастает (рис. 3.3) до определенного предела (устойчивое равновесие, точка пересечения биссектрисы с параболой) (рис. 3.3, 3.4).

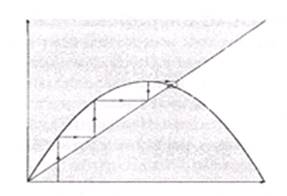
Рис. 3.3                                         Рис. 3.4

Если r > 2, то процесс начинает осциллировать (возникают колебания, бифуркации значений) сначала между двумя (рис. 3.5, 3.6), а потом четырьмя (рис. 3.7), восьми и т. д. уровнями (происходит последовательное удвоение периода колебаний).

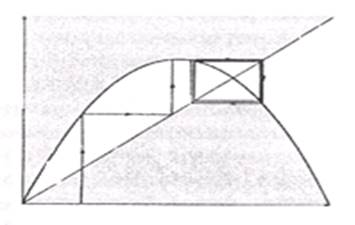
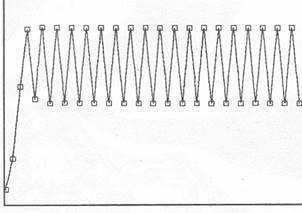
Цикл периода 2

Рис. 3.5                                                          Рис. 3.6

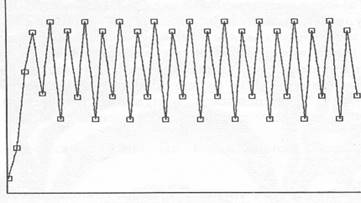
Рис. 3.7 (цикл периода 4)

Если  – значение параметра роста, соответствующее n-ой бифуркации, когда происходит смена периодов колебаний, то  сходится к значению 4,669…, когда  («число Фейгенбаума»). Удвоение периода напоминает фрактал, основанный на двоичной системе с показателем масштабирования, равным числу Фейгенбаума.

Наконец, при  процесс становится «хаотическим»:

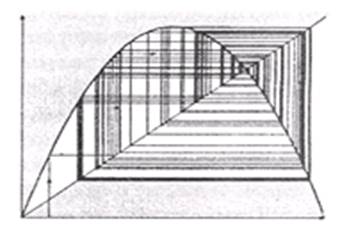
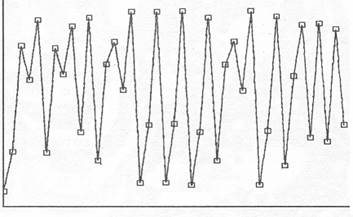
Рис. 3.8                                                     Рис. 3.9

Внутри «хаотической» области существует бесчисленное множество «окон» с  устойчивыми периодическими точками. Структура каскада бифуркаций за точкой хаоса  соответствует структуре каскада бифуркаций, предшествующего ей (так называемый обратный каскад). Около точки  полного хаоса () имеется только одна хаотическая полоса, распадающаяся при  на две, при  на четыре, затем на 8,16,32 полос и т.д. до бесконечности. Область  - область «детерминированного хаоса» с окнами устойчивости. Ниже представлена бифуркационная диаграмма (зависимость  от r). Следует отметить, что рассматриваемые колебания являются не переходным режимом, а установившимися (стационарными) колебаниями.

Рис. 3.10 Бифуркационная диаграмма

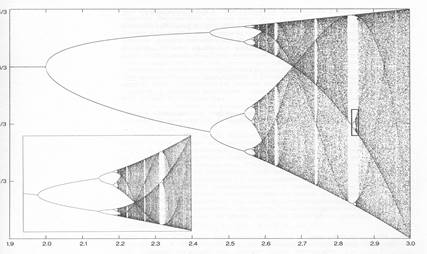
«Хаотическое» поведение нелинейной системы – не аналог случайного ее поведения, так как процесс полностью воспроизводим, он предопределен уравнением состояния, то есть детерминирован. Это «детерминированный хаос» - характерное свойство нелинейных систем.

Очевидно, что не только экономический, но также и социально-экономический процесс можно записать как химическую автокаталитическую реакцию. Например, если вместо исходных реагентов подразумевать жизненные блага и работников, а вместо продуктов реакции – работников (конечной целью всякого производства является воспроизводство рабочей силы), то можно построить модель изменения народонаселения. Например, итерационное уравнение

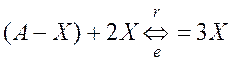
означает, что производственная деятельность двух работников (например, молодой семьи) при ограниченных ресурсах в состоянии обеспечить существование трёх человек (родить ребенка и воспитать из него квалифицированного работника).

3.3. Вопросы для самоконтроля

1.  Почему законы молекулярной химии выполняются в экономике и социологии?

2.  Описывается ли вся сложность экономической и социально-экономической жизни законами химии?

3.  Приведите другие примеры действия физико-химического закона Ле Шателье в экономике и обществе.

4.  Используйте химический закон  действующих масс для объяснения и описания других экономических и социально-экономических процессов.

5.  Приведите примеры выполнения в экономике и социологии других физических и химических законов (например, газовых законов).