Товарное хозяйство – нелинейная динамическая система, страница 38

В настоящее время в прикладной науке господствуют стохастические  модели, в основе которых лежит допущение о независимости событий, а вероятность распределения событий описывается симметричной «колоколообразной» кривой К. Гаусса с быстро спадающими хвостами (классическая статистика). Эта кривая базируется на принципах относительного «равноправия», «равнозначности» (каждое событие вносит вклад в общую сумму, но ни одно из них не определяет статистический результат).

Уравнение кривой Гаусса

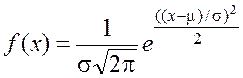, где х – уровень  исследуемой величины; μ – среднее значение всех величин; σ – стандартное отклонение, то есть ширина разброса величин вокруг среднего значения.

Известна также статистика Коши, Леви, Парето и других со степенным (гиперболическим) законом распределения. В статистике Коши уравнение для приведенной плотности вероятности:

.

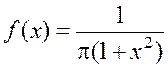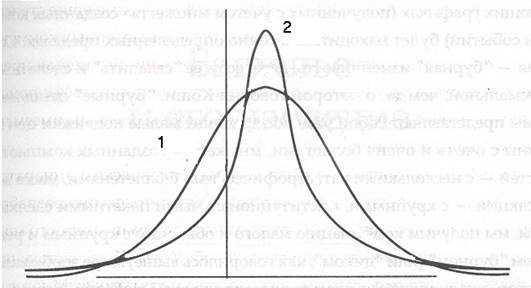
Рис 8.1 Кривая Гаусса (1), кривая Коши (2, пример - стрельба из лука вслепую, пики - островершинные, хвосты – «толстые»).

В статистике Коши-Леви «колоколообразная» кривая приподнята над осью абсцисс и, следовательно, имеет так называемые «толстые» или «жирные» хвосты, что означает существование бесконечной дисперсии.

Итальянец Вильфредо Парето еще в 1897 г. показал, что распределение доходов среди населения во всех странах и во все эпохи не подчиняется «нормальному» закону, а кривая доходов среди богатых описывается степенной формулой (гиперболическим законом):

,

где х – величина дохода, у – количество лиц, имеющих доход, превышающий х, a– минимальный доход,  А и  α – параметры зависимости, получаемой статистически.

В логарифмических осях (дважды логарифмический или билогарифмический график) формула описывает прямую линию с наклоном. Степенная функция - свидетельство, что использование ресурса системой зависит от величины ее ресурса (обратная связь).

Распределение типа  характерно не только для доходов богатых (Парето),  но и частотности слов (Ципф), научных публикаций (Лотка), размера городов (Саймон), финансовых рынков (Мандельброт). В частности, Мандельброт показал, что доходность акций характеризуется гиперболическим распределением, имеющем «жирные» хвосты и бесконечную дисперсию.

Опыт показывает, что экспериментальные стохастические результаты стремятся, в основном, к распределениям, описываемым именно этими двумя законами: «нормальным» законом Гаусса (равнозначные события, однородные системы) и степенным законом (неравнозначные события, неоднородные системы. Согласно Мандельброту рассматриваемые два типа распределений – это две крайности, которые  целым спектром других членов семейства связывает распределение Леви: 

, имеющее четыре ключевых переменных, определяющих окончательную форму кривой (Гаусса, Парето и др.): δ – параметр “местоположения”, γ – параметр масштаба (определяет величину общей вероятности), β – параметр ассиметричности (при β = 0 кривая симметрична),  α – параметр, который определяет “толщину хвостов”. Если α = 2, а  β = 0, то распределение Леви описывает стандартную кривую (Гаусса), при α = 1, а  β = 0  - кривую Коши с очень “толстыми хвостами”.

Бенуа Мандельброт является основоположником фрактальной геометрии, Он  показал, что гиперболические распределения – «ближайшие родственники фракталов» (в какой-то степени самоподобных структур), что они статистически самоподобны (масштабно-инвариантны) и назвал такую статистику фрактальной. Им введено понятие фрактальной размерности пространства вероятностей. В гиперболических распределениях роль размерности играет показатель степени.

Мандельброт пришел к выводу, что имеют место три состояния «случайности». Он ввел понятия «мягкой», «медленной» и «бурной» случайности и попытался провести их аналогию с агрегатными состояниями вещества (твердым, жидким и газообразным), то есть использовать для описания случайных событий, в том числе финансово-экономических событий, представления физики как точной науки о веществе.

Более широкая идея называть преобразующее природу человечество «живым веществом» принадлежит Вернадскому. Субъекты хозяйствования часто называют «молекулами» (например, лауреат Нобелевской премии по Экономике Коуз).