Характеристики детерминированных сигналов. Представление произвольного сигнала в виде суммы элементарных колебаний

Глава 1

характеристики детерминированных

сигналов

В радиотехнике приходится иметь дело с электрическими сигналами, являющимися функциями времени – электрическими колебаниями различной формы.

Электрические сигналы бывают детерминированные и случайные. Детерминированным называют сигнал, мгновенные значения которого можно предсказать с вероятностью единица. Примерами детерминированных сигналов являются импульсы или пачки импульсов, форма, амплитуда и положение во времени которых известны, а также непрерывный сигнал с заданными амплитудными и фазовыми соотношениями внутри его спектра. Детерминированные сигналы бывают периодические и непериодические.

Периодическим называется любой сигнал, для которого выполняется условие , где период колебания Т является конечным отрезком, а k – любое целое число.

Простейшим периодическим детерминированным сигналом является гармоническое колебание (ток, напряжение, напряжённость поля, заряд), определяемое выражением

,

-∞<<∞,                                       (1)

где A, T,  и  - постоянные амплитуда, период, угловая частота и начальная фаза колебания.

Любой сложный периодический сигнал, можно представить в виде суммы гармонических колебаний с частотами, кратными основной частоте . Основной характеристикой сложного периодического сигнала является его спектральная функция, содержащая информацию об амплитудах и фазах отдельных гармоник.

Непериодическим детерминированным сигналом называется любой детерминированный сигнал, для которого не выполняется условие

.

Обычно, непериодический сигнал ограничен во времени. Примерами таких сигналов являются уже упомянутые выше импульсы, пачки импульсов, гармонические колебания, заданные на конечном интервале времени и т.д. Непериодические сигналы представляют главный интерес, так как в основном применяются в практике.

Основной характеристикой непериодического, как периодического сигнала, является его спектральная функция. При этом структура спектра непериодического сигнала имеет ряд особенностей, которые будут рассмотрены в настоящем разделе.

К случайным сигналам относятся сигналы, значения которых заранее неизвестны и могут быть предсказаны с вероятностью меньшей единицы. К таким сигналам являются электрическое напряжение, соответствующее речи, музыке и т.д.

Для характеристики и анализа случайных сигналов применяется статистический метод, в котором в качестве основных характеристик принимают закон распределения вероятностей и спектральное распределение мощности сигнала.

Наряду с полезными случайными сигналами в радиотехнике приходится иметь дело со случайными помехами – шумами. Уровень шумов является основным фактором, которым ограничивается скорость передачи информации при заданном сигнале.

1.1. Представление произвольного сигнала в виде суммы элементарных колебаний

В радиотехнике широко применяется разложение заданной функции  по различным ортогональным системам функций . Рассмотрим основные определения, относящиеся к свойствам ортогональных функций.

Бесконечная система действительных функций

,                                                                  (2)

называется ортогональной на интервале времени , если

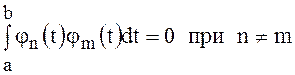.                                                                (3)

Это условие характеризует попарную ортогональность базисных функций системы (2).

Величина 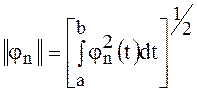                                                                (4)

называется нормой функции . При этом предполагается, что никакая из базисных функций системы (2) не равна тождественно нулю, т.е. .

В высшей математике доказывается, что если функции  непрерывны, то произвольная кусочно-непрерывная функция , для которой выполняется условие

,

где интеграл вычисляется по области определения функции , может быть представлена в виде ряда

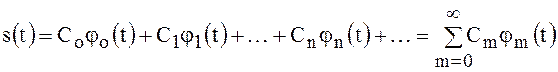.                   (5)

Умножим обе части уравнения (5) на  и проинтегрируем в пределах от a до b. Все слагаемые вида 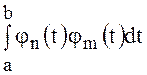 при  обращаются в нуль вследствие ортогональности базисных функций  и . В правой части уравнения остаётся одно слагаемое

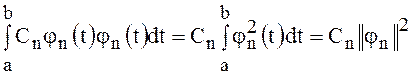, поэтому можно написать

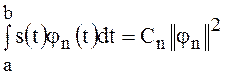, откуда следует важное соотношение

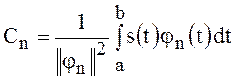.                                                                         (6)

Ряд (5), в котором коэффициенты  выражаются формулой (6), называется обобщённым рядом Фурье по данной системе базисных функций . Совокупность коэффициентов  называется спектром сигнала  в ортогональной системе базисных функций , полностью и определяет сигнал.

Обобщённый ряд Фурье обеспечивает минимальную среднеквадратичную ошибку аппроксимации данной функции  при заданной системе базисных функций  и фиксированном числе слагаемых ряда (5). Под среднеквадратичной ошибкой подразумевается величина .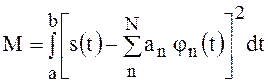

Величина М достигает минимума, если коэффициенты ряда :

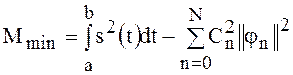.                                                                (7)

Так как 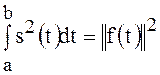, а , то на основании (7) можно написать.                                                                                                          (8)