Математическое ожидание и дисперсии. Приближённая формула Пуассона. Значение варьирующего признака, которое приходится на середину вариационного ряда

Вариант 2.

1. Абонент забыл шестизначный телефонный номер (первая цифра – не 0). Помнит только, что первые 2 цифры одинаковые, а другие – разные. Найти вероятность, что он дозвонится с первого раза.

Вероятность, что он отгадает первую цифру – 1/9. Вторую угадывать не надо (она совпадает с первой). Вероятности угадать каждую из последних чётырёх цифр – по 1/10. Таким образом, вероятность угадать все цифры одновременно:

2. Вероятность того, что нужная деталь лежит в первом ящике, составляет 0.7, во втором – 0.8, в третьем – 0.9. Найти вероятность того, что деталь лежит: а) только в одном ящике; б) не больше, чем в двух ящиках.

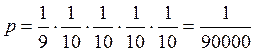
а) Итак, деталь может лежать либо в первом ящике и одновременно – не лежать во втором и третьем  (), либо лежать во втором ящике и не лежать в первом и третьем (), либо лежать в третьем и не лежать в первом и втором ().

Складывая эти вероятности, получим:

р=0.014+0.024+0.054=0.092

б) Единственный случай, когда условие не выполняется – когда деталь лежит в трёх ящиках одновременно. Поэтому вероятность того, что деталь лежит не более чем в двух ящиках, это, по сути, вероятность, того, что деталь НЕ лежит в трёх ящиках одновременно.

Вероятность того, что деталь лежит в трёх ящика одновременно, равна 0.7*0.8*0.9=0.504. Тогда нужная нам вероятность составляет 1-0.504=0.496.

3. Абонент пейджинговой связи не получает отправленное сообщение с вероятностью 0.1. Найти вероятность, что среди 80 отправленных сообщений будет а) ровно 6 не полученных; б) не больше 4 таких сообщений.

Поскольку количество независимых событий в серии велико (80), будем пользоваться приближённой формулой Пуассона:

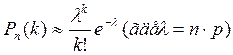
а) Согласно формуле

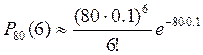, т.к. n – количество испытаний в серии (80), k - количество успехов (6, в нашем случае успехом будем считать неполучение сообщения), а вероятность успеха каждого испытания – p (0.1 т.к., опять же, успехом считаем неполучение сообщения).

Тогда P≈0,1221

б) Надо найти вероятность того, что недошедших сообщений будет или 0, или 1, или 2, или 3. Тогда

P=P₈₀(0)+ P₈₀(1) + P₈₀(2) + P₈₀(3)=

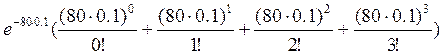=≈0,042380

4. В коробке 2 красных, 3 чёрных и 3 синих ручки. Наугад выбирают 2 ручки, и Y – количество синих среди них. Найти распределение Y, его математическое ожидание и дисперсию.

Для того, чтобы найти функцию распределения, найдём вероятности того, что Y равно 0, 1 и 2.

Вероятность того, что Y=0

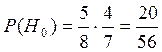, т.к., когда мы вытаскиваем первую ручку – их в коробке 8, из них 5 – не синих, а когда вытаскиваем вторую – всего 7 ручек, из которых не синих – 4.

Вероятность того, что Y=1

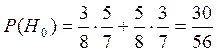, т.к.:

1) либо, когда мы вытаскиваем первую (синюю) ручку – их в коробке 8, из них 3 – синих, а когда вытаскиваем вторую (уже не синюю) – всего 7 ручек, из которых не синих – 5;

2) либо, когда мы вытаскиваем первую (не синюю) ручку – их в коробке 8, из них 5 – не синих, а когда вытаскиваем вторую (уже синюю) – всего 7 ручек, из которых синих – 3.

Вероятность того, что Y=2

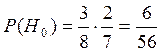, т.к., когда мы вытаскиваем первую ручку – их в коробке 8, из них 3 – синих, а когда вытаскиваем вторую – всего 7 ручек, из которых синих осталось – 2.

Так как значение функции распределения – это сумма вероятностей появления величин, умноженных на отрезок, на котором достигается величина (все такие отрезки у нас равны 1, т.к. у нас вероятности посчитаны для величин Y, которые отличаются на единицу), то, для х<0, F(x)=0, для 0<=x<=1, F(x)=

для 1<x<=2, F(x)=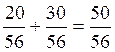

для x>2, F(x)=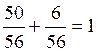

Окончательно:

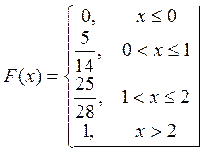
Для математического ожидания и дисперсии воспользуемся следующими формулами:

 и

5. Фермер выращивает цыплят. Месячные цыплята в среднем весят 0.8 кг, а среднеквадратичное отклонение веса 0.2. Найти вероятность того, что каждый из двух наугад выбранных цыплят весит больше, чем 0.75.

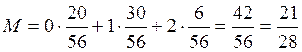
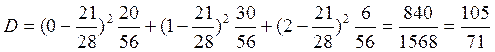
Для начала найдём вероятность того, что один наугад выбранный цыплёнок весит меньше, чем 0.75. Вероятность этого – значение функции распределения F(x) (в данном случае – распределения веса) в точке 0.75.

Так как

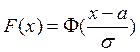, где Φ – функция нормального распределения с мат. ожиданием=0 и дисперсией=1,

a – мат. ожидание нашего распределения (среднее)

σ – среднеквадратичное отклонение нашего распределения

Тогда 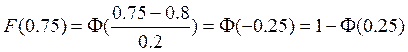={определяем по таблице}=

=1-0,5987=0,4013.

/*в таблицах учебников можно встретить функцию распределения Φ, для которой Φ(0.25)=0.0987. Будьте внимательны: там интеграл от нуля до х, а нам нужна функция с интегралом от (–бесконечности) до х, и её значение равно 0.5 + (значение функции, где интеграл взят от нуля до х)*/

Это мы нашли вероятность того, что цыплёнок весит меньше, чем 0.75. А вероятность того, что он весит больше, равна

p₁=1-F(0.75)=0.5987.

А вероятность того, что из двух наугад выбранных цыплят оба одновременно весят меньше, чем 0.75, равна

p=p₁*p₁=0.5987*0.5987=0,35844169

6. Проводилось измерение веса 36 наугад выбранных студентов 1-го курса: (кг): 69, 75, 59, 80, 52, 53, 60, 73, 52, 63, 71, 69, 58, 53, 65, 61, 67, 65, 74, 63, 68, 70, 72, 66, 62, 54, 58, 60, 72, 62, 64, 68, 59, 58, 55, 54. Построить вариационный ряд, эмпирическую функцию распределения, интервальное распределение, гистограмму частот. Вычислить среднее, выборочную дисперсию, среднеквадратичное распределение, медиану. Найти доверительный интервал для среднего.