Вариационный ряд – это отсортированный по возрастанию ряд выборочных значений:
52, 52, 53, 53, 54, 54, 55, 58, 58, 58, 59, 59, 60, 60, 61, 62, 62, 63, 63, 64, 65, 65, 66, 67, 68, 68, 69, 69, 70, 71, 72, 72, 73, 74, 75, 80.
Эмпирическая функция (правила построения смотри в зад.4):
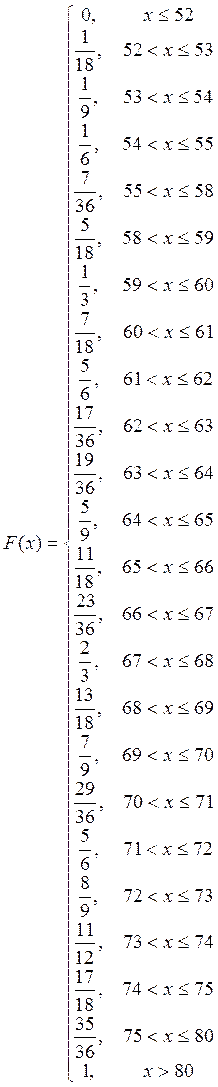
Интервальное распределение:
|
Ii |
52:55 |
55:58 |
58:61 |
61:64 |
64:67 |
67:70 |
70:73 |
73:76 |
76:80 |
|
mi |
7 |
3 |
5 |
5 |
4 |
5 |
4 |
2 |
1 |
|
Wi=mi/n |
0.1944 |
0.0833 |
0.1389 |
0.1389 |
0.1111 |
0.1389 |
0.1111 |
0.2222 |
0.1111 |
Гистограмма частот:
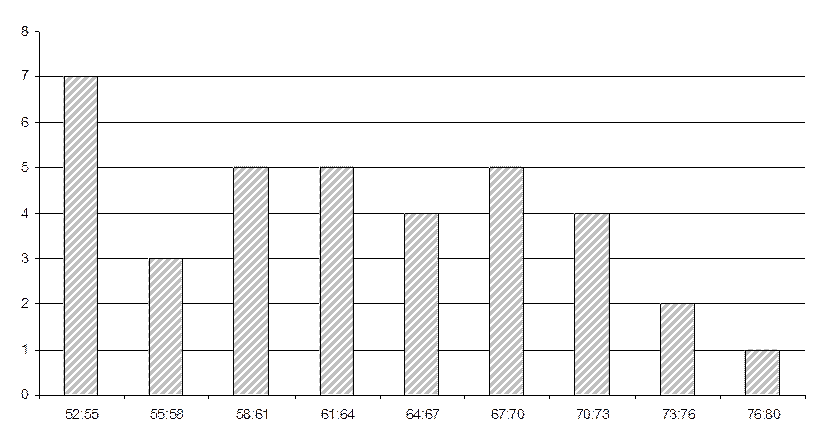
Выборочное среднее:
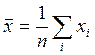=63.4444
Выборочная дисперсия:
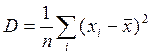=52,1358
Среднее квадратическое отклонение:
=7,220513
Медианой называется такое значение варьирующего признака, которое приходится на середину вариационного ряда. В нашем случае число вариант – чётно, поэтому берётся среднее двух серединных элементов вариационного ряда:
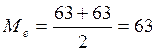
Доверительный интервал для среднего (при заданной надёжности γ) имеет вид
(
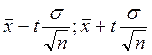), где t – значение
аргумента функции Лапласа Φ(t), при котором Φ(t)= γ/2
/*тут имеется в виду функция распределения, у которой интеграл берётся от нуля до х*/
Возьмём надёжность 0.95. Тогда (по находим по таблице) Φ(1.96)=0.95/2, значит t=1.96 и доверительный интервал будет
(
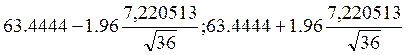) или
a принадлежит
интервалу (
)
Вариант 4.
а)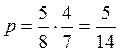 
т.к. когда берём первую книгу, на
полке стоят 8 книг, 5 из которых – по математике, а когда берём вторую – 7
книг, из которых осталось 4 по математике.
б)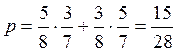 
, т.к. мы либо первой достаём
первой одну из 5 книг по математике среди 8ми на полке, а второй – одну из 3х
книг по физике среди оставшихся 7ми на полке, либо первой достаём
одну из 3 книг по физике среди 8ми на полке, а второй – одну из 5ти книг по
математике среди оставшихся 7ми на полке.
а) Т.к. одно должно быть первого сорта, и, одновременно, второе – не первого сорта, перемножаем вероятности этих событий:
p=0.25*(1-0.25)
б) Аналогично, вероятность, что оба – высшего сорта, = 0.7*0.7, что оба – первого сорта, = 0.25*0.25, и что оба – «оставшегося» сорта, = 0.05*0.05 (раз 95% продукции – либо первый, либо высший сорт, то должны быть ещё 5% какого-то «третьего» сорта), тогда вероятность, что произойдёт одно из этих событий – сумма их вероятностей:
p=0.72+0.252+0.052=0.555
а) Очевидно, что вероятность одного промаха и, одновременно с этим, шести попаданий равна:
p=(1-0.7)*0.76=0,0352947
б) Так как количество событий велико, воспользуемся приближённой формулой Пуассона:
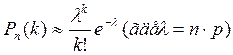
Получим
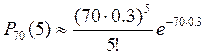, т.к. n=70 – количество
испытаний в серии, k=5 - количество успехов (успехом будем
считать промах), а вероятность успеха каждого испытания – p=0.7.
Вычисляя, получим:
P70(5)≈0.0000258
Для того, чтобы найти функцию распределения, найдём вероятности того, что Х равно 0, 1, 2 и 3.
Вероятность того, что Х=0
Р(Н0)=0.4*0.5*0.5=0.1 – все монеты выпали «решкой»
Р(Н1)=0.6*0.5*0.5 + 0.4*0.5*0.5 + 0.4*0.5*0.5=0.35 – либо первая выпала решкой (остальные - гербами), либо вторая (остальные - гербами), либо третья (остальные - гербами).
Р(Н2)=0.6*0.5*0.5 + 0.4*0.5*0.5 + 0.6*0.5*0.5=0.4 – либо первая и вторая выпали решкой (третья - гербом), либо вторая и третья (первая - гербом), либо первая и третья (вторая - гербом).
Р(Н3)=0.6*0.5*0.5=0.15 – все выпали гербом
Так как значение функции распределения – это сумма вероятностей появления величин, умноженных на отрезок, на котором достигается величина (все такие отрезки у нас равны 1, т.к. у нас вероятности посчитаны для величин Х, которые отличаются на единицу), то, для х<0, F(x)=0, для 0<=x<=1, F(x)= 0.1
для 1<x<=2, F(x)= 0.35+0.1=0.45
для 2<x<=3, F(x)= 0.4+0.45=0.85
для x>3, F(x)= 1
Окончательно:
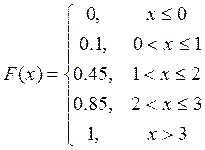
Для математического ожидания и дисперсии воспользуемся следующими формулами:
и 
М=0*0.1+1*0.35+2*0.4+3*0.15=1.6
D=(0-1.6)20.1+(1-1.6)20.35+(2-1.6)20.4+(3-1.6)20.15=0,584
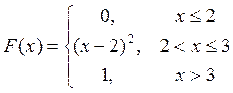
По определению
Р{2<x<2.5}=F(2.5)-F(2)=(2.5-2)2-0=0.25
6. (см. выше - вариант 2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.