1.
При ![]() автокорреляционная
функция положительна и имеет наибольшее значение.
автокорреляционная
функция положительна и имеет наибольшее значение.
2.
Автокорреляционная функция
является чётной функцией временного сдвига ![]() :
:
![]() .
Поэтому знак минус перед
.
Поэтому знак минус перед ![]() в
выражении (87) можно изменить на плюс, записав
в
выражении (87) можно изменить на плюс, записав
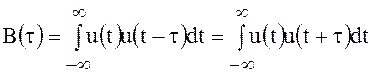 .
(93)
.
(93)
На рис. 17 а, показано построение корреляционной функции для прямоугольного импульса.

Рис. 17 а
Сдвинутый на время ![]() ( в сторону
опережения)сигнал
( в сторону
опережения)сигнал ![]() показан на
рис. 17 б, а произведение
показан на
рис. 17 б, а произведение ![]() -
на рис. 17 в. Каждому значению
-
на рис. 17 в. Каждому значению ![]() соответствует
своё произведение
соответствует
своё произведение ![]() , а
площадь, ограниченная функцией
, а
площадь, ограниченная функцией ![]() ,
даёт ординаты корреляционной функции
,
даёт ординаты корреляционной функции
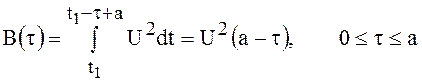 .
.
График функции ![]() представлен на рис. 17
г.
представлен на рис. 17
г.

17 б
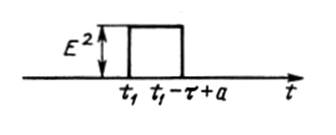
17 в

17 г
Энергия периодического сигнала равна бесконечности, поэтому его энергетические свойства характеризуются мощностью, т.е. отношением энергии за некоторый промежуток времени к длительности этого промежутка. Аналогично определяется и автокорреляционная функция периодического сигнала:
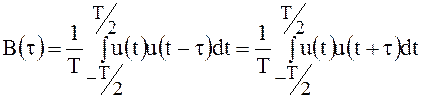 ,
(91)
,
(91)
где Т – период функции ![]() .
.
Важную роль играет связь между энергетическим спектром
![]() и автокорреляционной
функцией
и автокорреляционной
функцией ![]() .
.
Подставляя в выражение (90) сигнал ![]() в виде обратного
преобразования Фурье, получим
в виде обратного
преобразования Фурье, получим
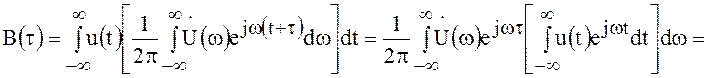
 . (92)
. (92)
Следовательно, автокорреляционная функция ![]() является обратным
преобразованием Фурье от энергетического спектра
является обратным
преобразованием Фурье от энергетического спектра 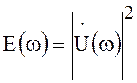 .
.
Прямое преобразование Фурье от автокорреляционной функции сигнала определяет его энергетический спектр
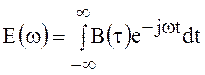 .
(93)
.
(93)
Выражения (91) и (92), устанавливающие связь между автокорреляционной функцией и его энергетическим спектром, называются соотношениями Винера-Хинчина.
Кроме автокорреляционной функции можно определить также взаимно корреляционную функцию
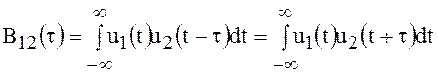 .
(94)
.
(94)
Взаимно корреляционная функция характеризует взаимную связь между значениями двух вещественных сигналов.
Когда ![]() и
и
![]() - один и тот же
сигнал, то взаимно корреляционная и автокорреляционная функции совпадают.
- один и тот же
сигнал, то взаимно корреляционная и автокорреляционная функции совпадают.
Максимум взаимно корреляционной функции двух
одинаковых сигналов имеет место при ![]() .
Для различных сигналов
.
Для различных сигналов ![]() и
и ![]() максимум функции
может достигаться не при
максимум функции
может достигаться не при ![]() .
.
Построение взаимно-корреляционной функции для двух
сигналов ![]() и
и ![]() приведено на рис.
18. Исходное положение сигналов
приведено на рис.
18. Исходное положение сигналов ![]() изображено
на рис. 18a. При сдвиге сигнала
изображено
на рис. 18a. При сдвиге сигнала ![]()
![]() влево
влево ![]() корреляционная функция сначала возрастает,
затем убывает до нуля при
корреляционная функция сначала возрастает,
затем убывает до нуля при ![]() .
При сдвиге вправо
.
При сдвиге вправо ![]() корреляционная
функция сразу убывает. В результате получается асимметричная относительно оси
ординат функции
корреляционная
функция сразу убывает. В результате получается асимметричная относительно оси
ординат функции ![]() .
.
![]()
Рис. 18
1.8. Дискретизованные сигналы
Процедуру дискретизации (взятие отчётов), осуществляемую
с помощью электронного ключа, можно рассматривать как умножение функции
аналогового сигнала ![]() на
вспомогательную функцию
на
вспомогательную функцию ![]() (см.
рис. 19):
(см.
рис. 19):
![]() ,
(95)
,
(95)
где ![]() - периодическая
последовательность прямоугольных тактовых импульсов, имеющих длительность
- периодическая
последовательность прямоугольных тактовых импульсов, имеющих длительность ![]() и период повторения
Т, равный шагу дискретизации
и период повторения
Т, равный шагу дискретизации ![]() .
.
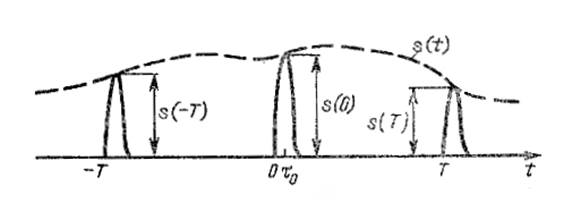
Рис. 19
Спектральную плотность исходного аналогового сигнала ![]() будем считать
заданной.
будем считать
заданной.
Представим периодическую функцию ![]() в виде ряда Фурье, в
котором скважность импульсов
в виде ряда Фурье, в
котором скважность импульсов 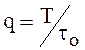 ,
а
,
а ![]() - частота повторения
импульсов
- частота повторения
импульсов ![]() :
:
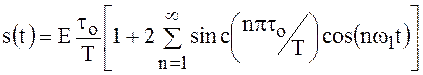 .
(96)
.
(96)
Подставим это выражение в формулу (95):
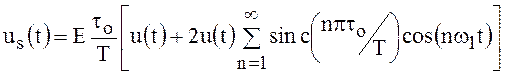 .
(97)
.
(97)
Спектр дискретного сигнала ![]() равен
равен

Первому слагаемому в правой части выражения (97) ![]() соответствует спектр
соответствует спектр
![]() исходного
аналогового сигнала, а каждому из произведений
исходного
аналогового сигнала, а каждому из произведений
![]() -
спектр
-
спектр 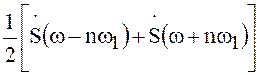 .
.
Следовательно, искомый спектр
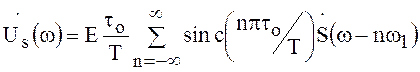 .
(98)
.
(98)
Графики функций ![]() и
и ![]() при шаге
дискретизации
при шаге
дискретизации 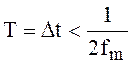 представлены
на рис. .20.
представлены
на рис. .20.
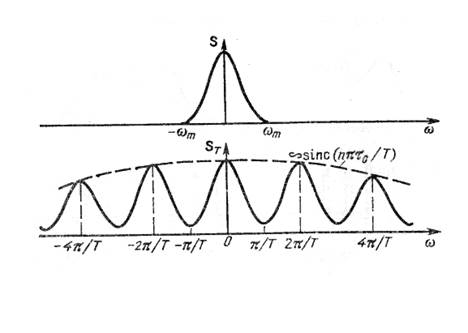
Рис. 20
Спектр ![]() дискретизованного
периодического сигнала представляет собой последовательность спектров
дискретизованного
периодического сигнала представляет собой последовательность спектров ![]() исходного
аналогового сигнала
исходного
аналогового сигнала ![]() , сдвинутых
один относительно другого на частоту
, сдвинутых
один относительно другого на частоту ![]() и
убывающий по закону
и
убывающий по закону 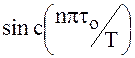 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.